一、市场类型的划分
在经济分析中,根据不同的市场结构的特征,市场可分为["完全竞争市场"]、["垄断竞争市场"]、["寡头垄断市场"]和["垄断市场"]四种类型。
市场划分依据:
- 市场上厂商数量;
- 商场生产产品的差别程度;
- 单个厂商对价格的控制程度;
- 厂商进入或退出行业的难易程度。

二、厂商的收益与利润
(一)厂商的收益
厂商的收益是厂商的销售收入:
总收益(\(TR\)):厂商按一定价格出售一定数量产品时获得的全部收入。\(TR(Q)=P \cdot Q\)
平均收益(\(AR\)):厂商在平均每一单位产品销售上所获得的收入。\(AR(Q)=\frac {TR(Q)} Q\)
边际收益(\(MR\)):厂商增加一单位产品销售所获得的总收入的增量。\(MR(Q)=\frac {\Delta TR(Q)} {\Delta Q} = \frac {d TR(Q)} {dQ}\)
(二)利润函数与利润最大化条件
利润函数:\(\pi (Q)=TR(Q)-TC(Q)\)
不论对哪种类型的厂商,利润最大化的条件都是 \(MR=MC\)。在短期生产中:
- 只要 \(MR>MC\),厂商扩大生产就有利可图,会选择增加产量;
- 只要 \(MR<MC\),厂商扩大生产就会减少利润,会选择减少产量;
- 当 \(MR=MC\) 时,厂商的利润达到最大(或亏损最小),不会选择增加或减少产量。
数学补充:
证明:厂商的利润最大化条件是 \(MR=MC\)
利润函数:\(\pi (Q)=TR(Q)-TC(Q)\)
将上式两边对产量 \(Q\) 求导数,可得一阶条件:\(\frac {d \pi (Q)} {dQ}=\frac {d TR(Q) } {dQ}- \frac {d TC(Q)} {dQ}=MR(Q)-MC(Q)\)
当 \(\frac {d \pi (Q)} {dQ}=0\) 时,厂商的利润最大,或亏损最小,此时:\(MR(Q)=MC(Q)\)
二阶条件即充分条件为:\(\frac {d \pi ^2 (Q)} {dQ^2} = {MR}'(Q)-{MC}'(Q) < 0\),即 \({MR}'(Q)<{MC}'(Q)\)
注:当 \(MR=MC\) 时,厂商不一定能获得利润,而是保证厂商处于由既定的成本状况与收益状况所决定的最好情况之中,此时厂商的可以获得最大利润或最小亏损。
三、完全竞争市场
(一)完全竞争市场的条件
- 厂商没有定价权:市场上有大量的买者和卖者,买者和卖者都是价格的接受者,单个买者与卖者不能影响市场交易价格与交易数量;
- 商品无差异:市场上每一个厂商提供的商品都是完全同质的,所有厂商提供的同类产品完全可替代;
- 产品与要素自由流通:所有的资源具有完全的流动性
- 完全信息:不存在信息不对称或信息不完全,每个消费者与生产者掌握所有与自己的经济决策相关的信息。
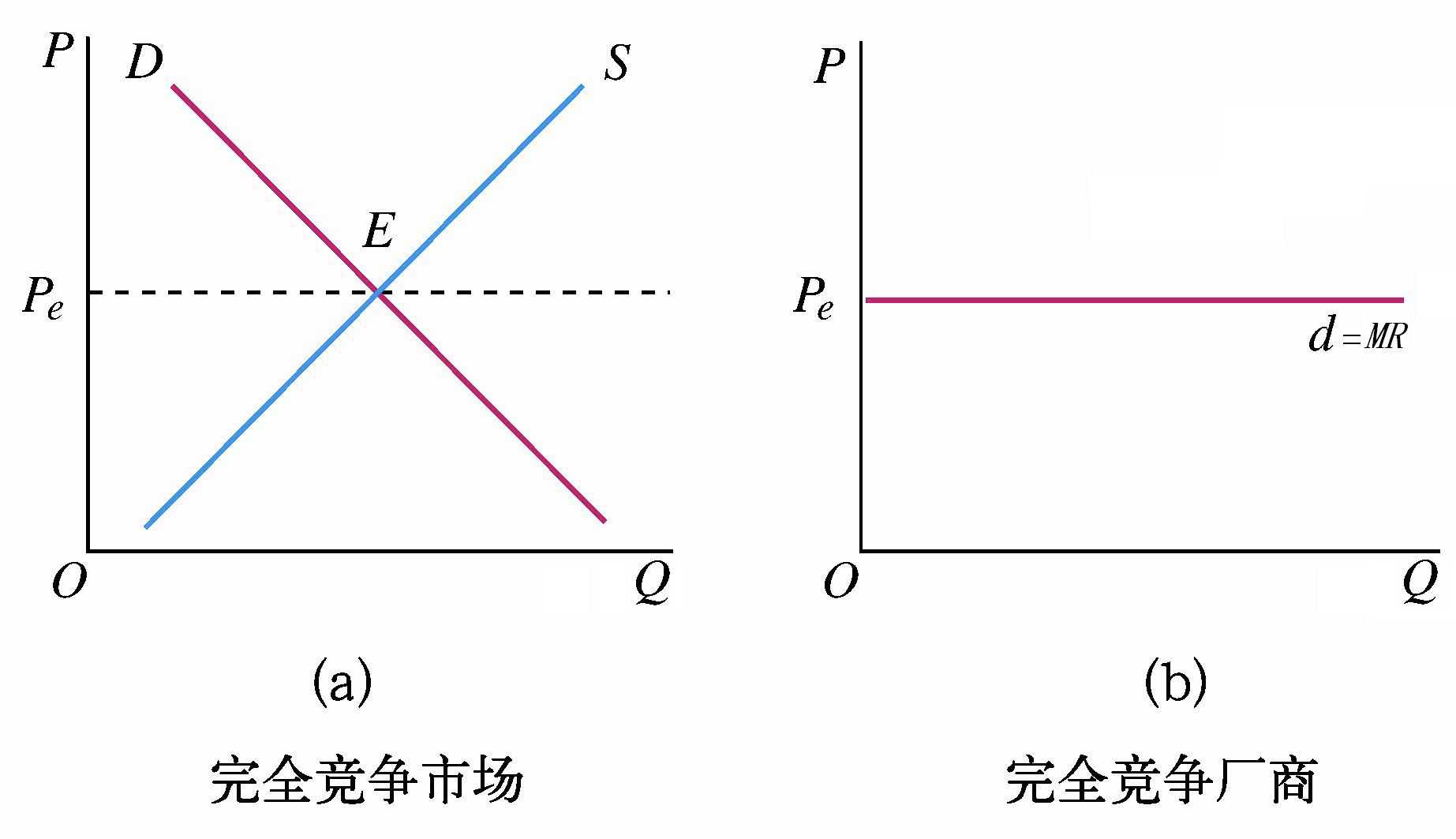
(二)完全竞争厂商的需求曲线
市场需求曲线是一条向右下方倾斜的曲线,单个企业所面临的需求曲线是一条由既定市场价格水平出发的水平线。
完全竞争市场的需求与供给决定价格,厂商根据价格作出生产决策(决定生产数量)。
消费者收入变化、新技术推广应用、政府相关政策等会影响完全竞争市场的供需关系,进而影响市场价格与厂商的生产决策。
完全竞争市场的需求曲线为该行业所有厂商的需求曲线之和。
(三)完全竞争厂商的收益曲线
1. 完全竞争厂商的收益曲线
总收益 \(TR\),当价格对于单个企业为常数(他是价格接受者)时,\(MR=\frac {dTR} {dQ}=\frac {d(P\cdot Q)} {dQ}=P\)
对于任何一个厂商来说,平均收益总是等于价格。因此,完全竞争厂商的需求曲线、平均收益和边际收益曲线三线合一,即 \(AR=MR=P\),都从同一价格水平出发。
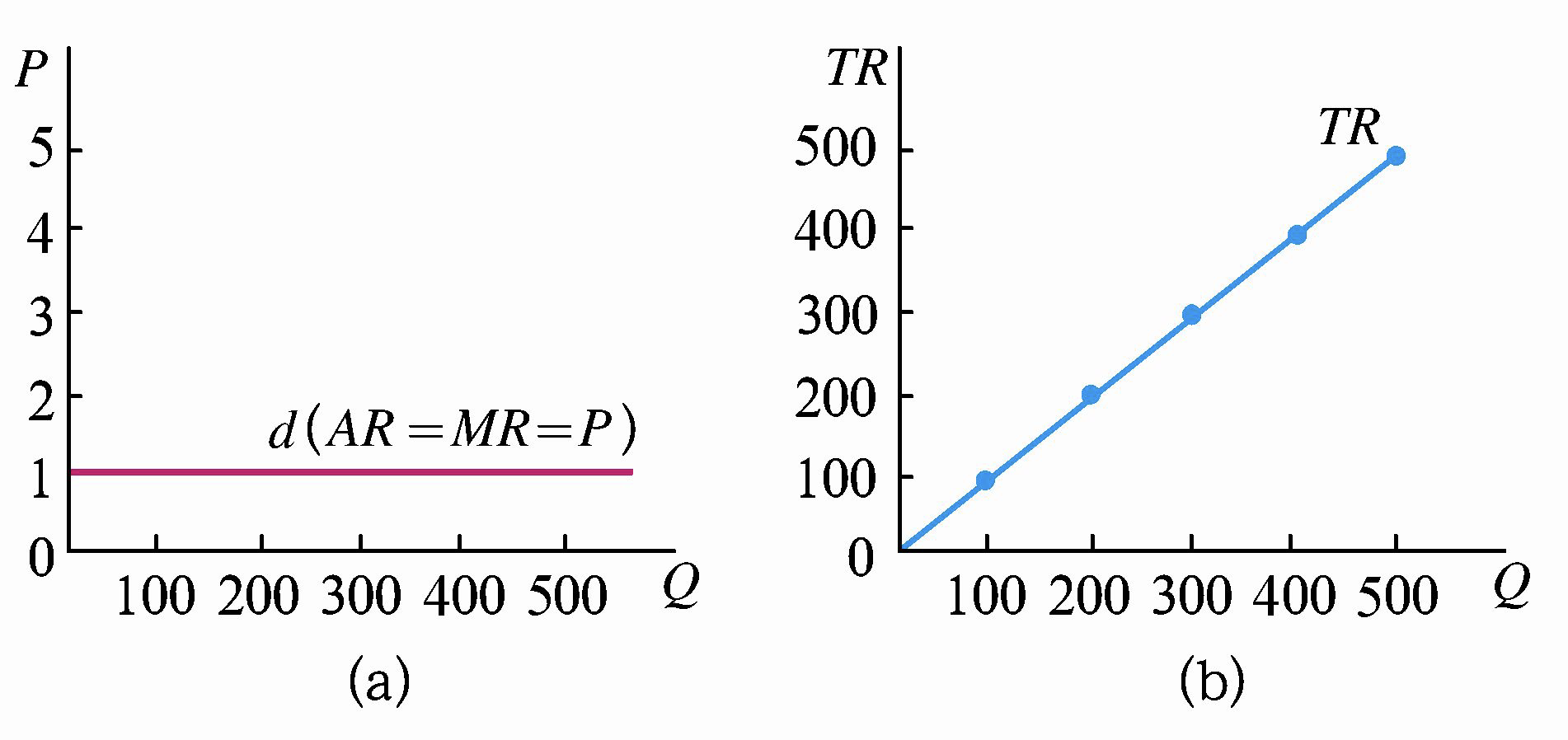
\(AR=P\) 在任何市场中都存在,但由于 \(MR=AR\) 仅有在完全竞争市场才可以成立,因此 \(AR=MR=P\) 三线合一仅有在完全竞争市场才会出现。
2. 利润最大化的短期均衡条件
厂商的["利润最大化条件"](短期均衡)为 \(MC=MR\),由于完全竞争厂商 \(AR=MR=P\),因此,短期内 \(P=MC(Q)\)。
对于完全竞争厂商来说,市场价格水平是给定的,单个厂商只能通过调整自身产量,使自身实现利润最大化。
3. 短期均衡的几种情况
在短期内,\(K=\overline K\),生产规模固定不变,因此厂商通过调整产量实现 \(MR=SMC\) 的利润最大化均衡条件。
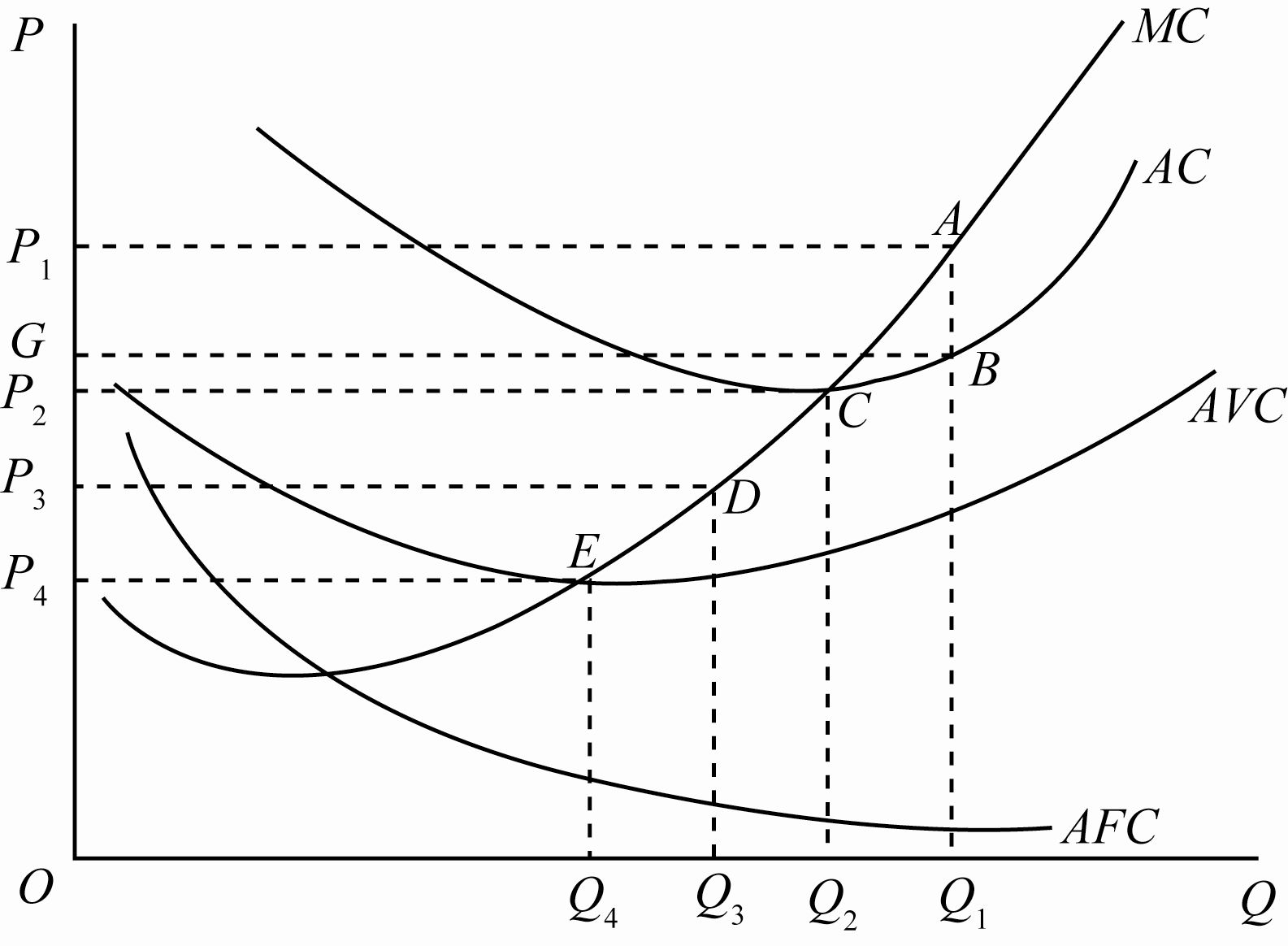
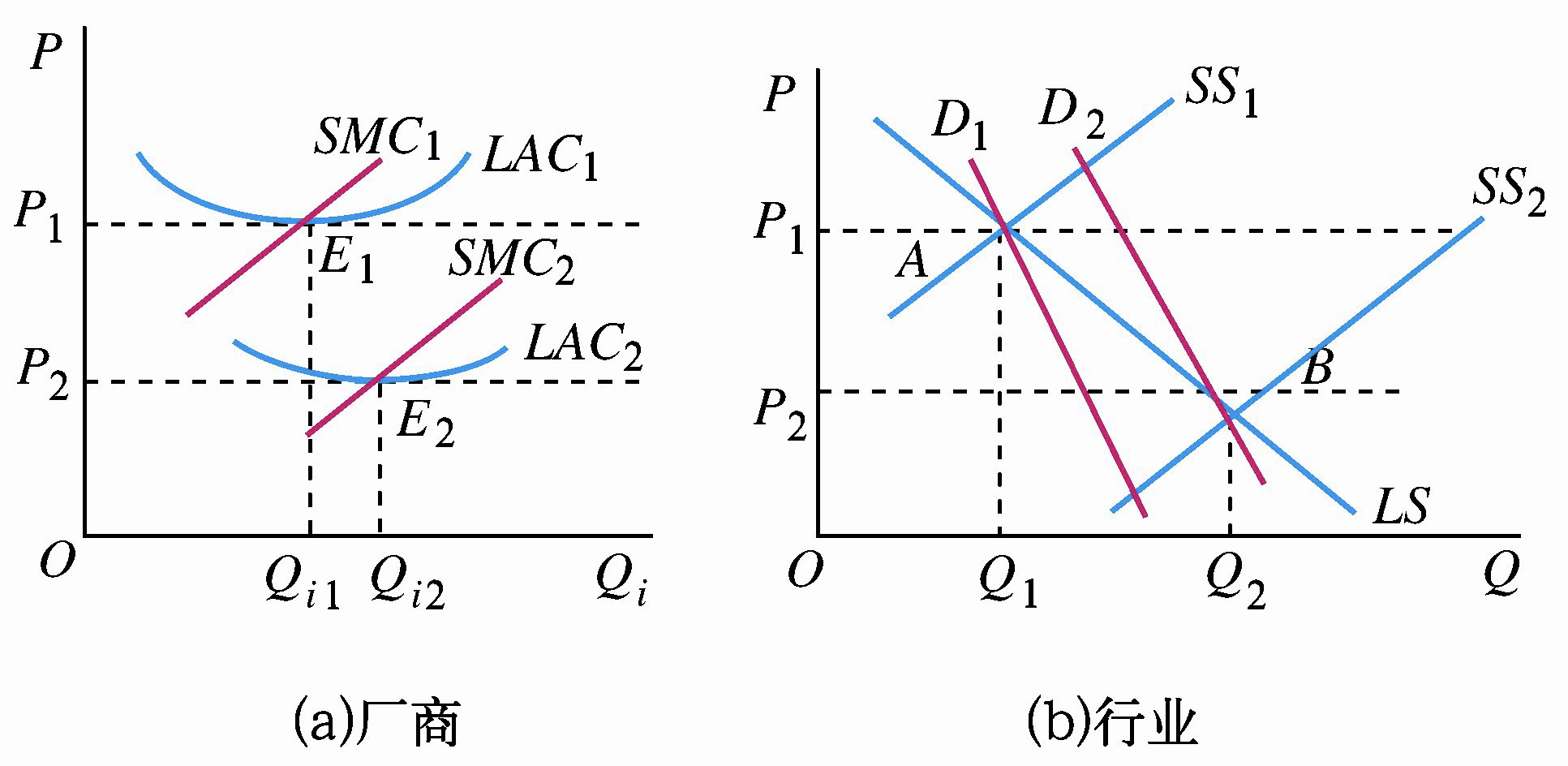
**情况 1:经济利润大于零的短期均衡。**价格为 \(P_1\) 时,\(MR\) 与 \(MC\) 相交于 \(A\) 点,此时 \(P_1>AC\),若按照产量 \(Q_1\) 生产,厂商可以获得矩形 \(ABP_1G\) 的超额利润。
**情况 2:经济利润等于零的短期均衡。**价格为 \(P_2\) 时,\(MR\) 与 \(MC\) 相交于 \(C\) 点,由于 \(C\) 点恰好是厂商 \(MC\) 与 \(AC\) 的交点,此时 \(P_2=AC\),若按照产量 \(Q_2\) 生产,厂商不能获得超额利润,但可以获得["正常利润"]。
**情况 3:亏损但继续生产经营的短期均衡。**价格为 \(P_3\) 时,\(MR\) 与 \(MC\) 相交于 \(D\) 点,由于 \(D\) 点处 \(P_3=MR<AC\),若按照产量 \(Q_3\) 生产,厂商将会亏损,但由于 \(P_3>AVC\),此时继续生产可以在支付可变成本的同时收回部分固定成本,可以减少亏损的金额(若不生产,将会亏损所有的固定成本),因此厂商会按照产量 \(Q_3\) 进行生产,此时厂商亏损最小。
**情况 4:亏损并停止生产经营的短期均衡(停止营业点)。**价格为 \(P_4\) 时,\(MR\) 与 \(MC\) 相交于 \(E\) 点,此时 \(E\) 点处 \(P_4=MR=AVC<AC\),厂商如果不生产,会亏损掉所有的固定成本,如果生产,按照产量 \(Q_4\) 生产的亏损最小,亏损额也是固定成本。因此厂商生产或不生产的亏损额度相同,厂商可以选择停止生产。
**情况 5:停止生产经营的短期均衡。**价格低于 \(P_4\) 时,厂商进行生产的 \(MR<AVC\),此时厂商如果选择不生产,将会亏损掉所有固定成本,如果生产,最小的亏损额度也超过固定成本。为追求亏损最少,厂商会选择不生产。
由此可以见,对于完全竞争厂商,\(MR=P\),完全竞争厂商生产由 \(MC=MR\) 确定的产量,是否有经济利润取决于平均成本 \(AC\) 与平均收益 \(AR\)(\(P=AR\))的大小比较;厂商是否选择停产,取决于生产的最小亏损是否小于固定成本,即价格 \(P\) 是否低于平均可变成本 \(AVC\)。
补充:
短期内,完全竞争厂商的经营决策依据:
- 确定产量:\(MR\) 与 \(MC\) 比较
- 是否盈利:\(AR\) 与 \(AC\) 比较
- 停产决策:\(MR\) 与 \(AVC\) 比较
(四)短期供给与短期均衡
1. 完全竞争厂商的短期供给曲线
根据上面 5 中情况的分析,可以推导出完全竞争厂商的短期供给曲线,为 SMC 曲线上大于和等于 AVC 曲线最低点的部分,即用 SMC 曲线大于和等于停止营业点的部分来表示。
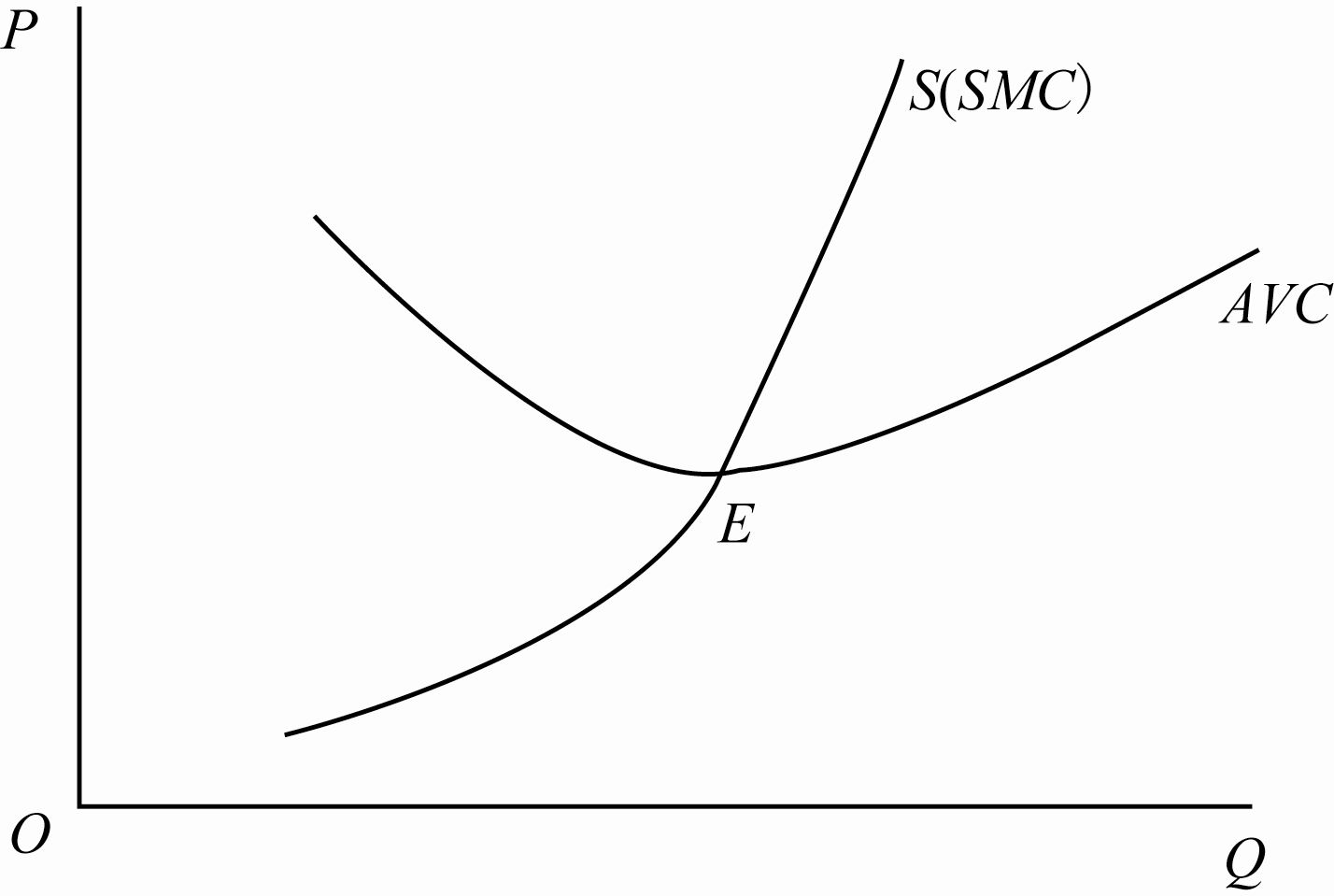
完全竞争厂商的短期供给曲线是向右上方倾斜的,它表示了商品的价格和供给量之间同方向变化的关系。==完全竞争厂商的短期供给曲线表示厂商在每一个价格水平的供给量都是能够给他带来最大利润或最小亏损的最优产量。==
2. 完全竞争市场的短期供给曲线
一个行业的短期供给曲线由该行业内所有厂商的短期供给曲线的水平加总而得到。行业的短期供给曲线也是向右上方倾斜的。
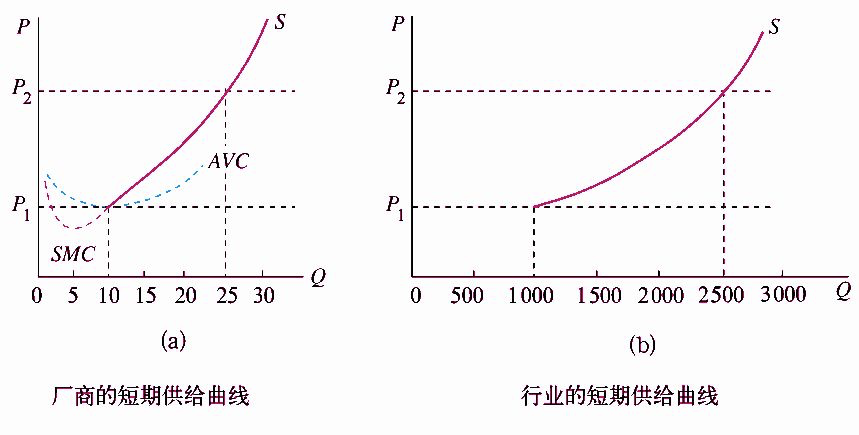
厂商的短期供给函数和行业的短期供给函数之间的关系用公式表示为:
\[\begin {align} S(P)=\sum^n_{i=1}S_i(P) \end {align} \]3. 短期生产者剩余
3.1 厂商的短期生产者剩余
在短期,厂商的生产者剩余指厂商在提供一定数量的某种产品时实际接受的总支付和愿意接受的最小总支付之间的差额。它通常用市场价格线以下、SMC 曲线以上的面积来表示。
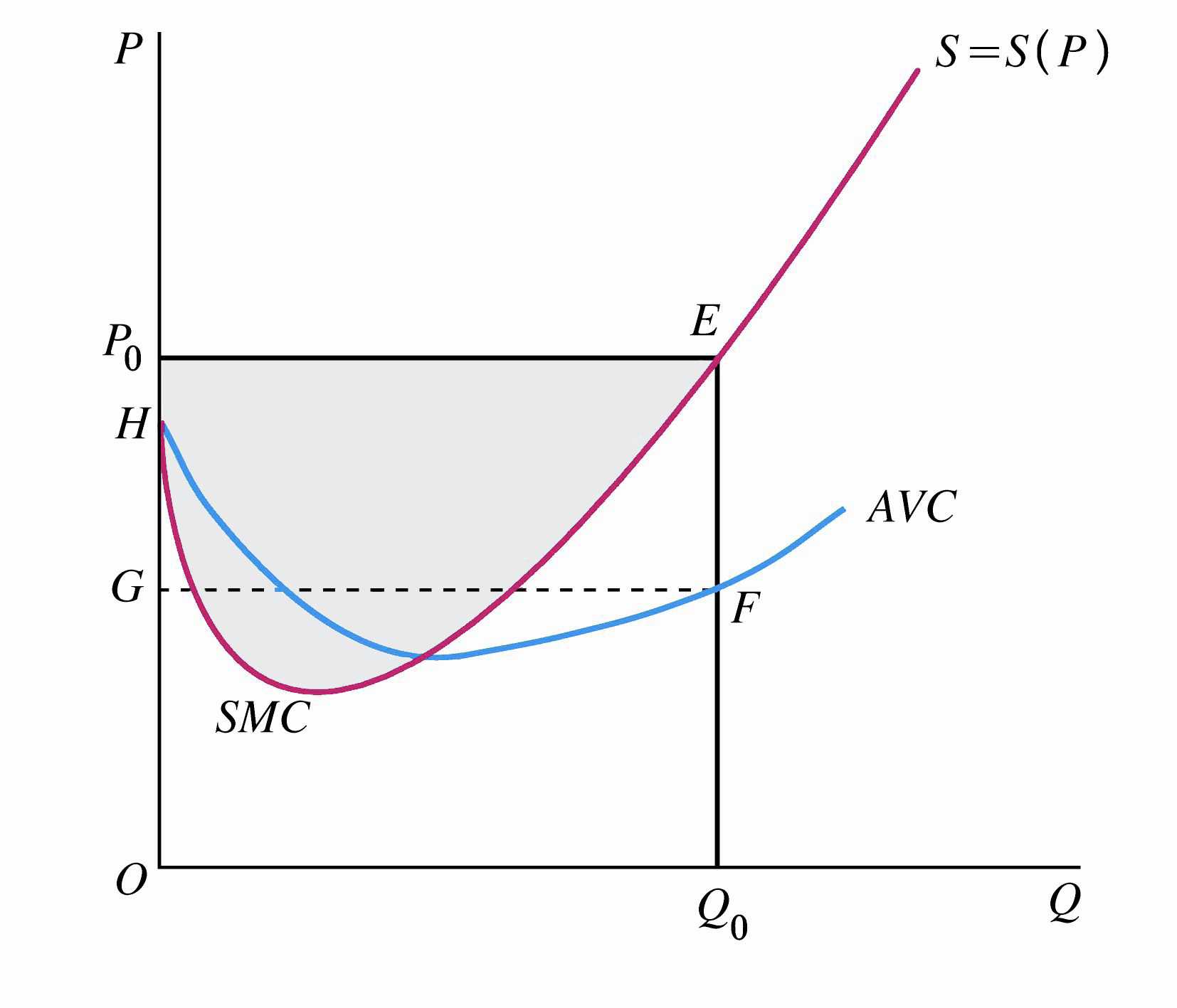
令反供给函数 \(P^S=f(Q)\),价格为 \(P_0\) 时厂商的供给量为 \(Q_0\),则厂商的短期生产者剩余为:
\[\begin{align} PS=P_0 \cdot Q_0 - \int^{Q_0} _0f(Q)dQ \end{align} \]==厂商的生产者剩余为图中的矩形 ====\(EFGP_0\)====。==原因在于:只要总收益大于总可变成本,厂商进行生产就是有利的(有正利润或减少固定投入的亏损),就能得到生产者剩余。生产者剩余\(PS\)可以表示为经济利润\(\pi\)与固定总成本\(TFC\)之和,即:\(PS=\pi +TFC\)。
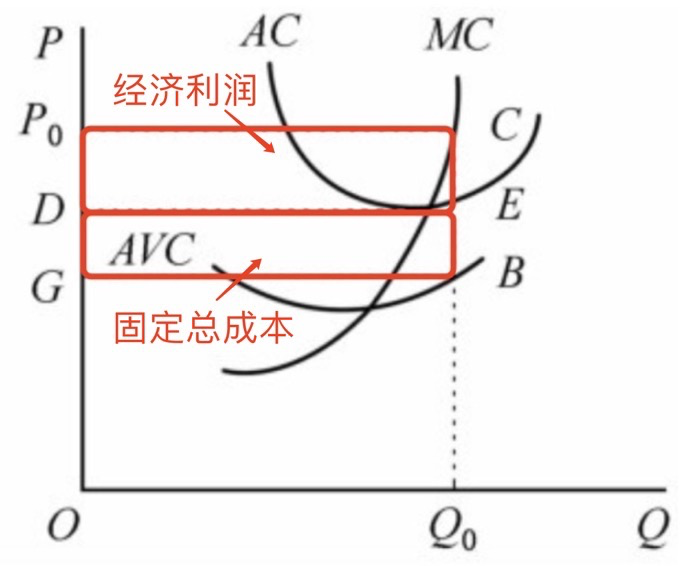
3.2 市场的短期生产者剩余
市场的生产者剩余是市场上所有厂商的生产者剩余的加总,用市场价格线以下、行业的短期供给曲线以上的面积来表示。
(五)长期供给与长期均衡
1. 完全竞争厂商的长期均衡
在长期中,所有的生产要素投入量都是可变的,完全竞争厂商通过对全部生产要素投入量的调整来实现利润最大化。在完全竞争市场价格给定的条件下,厂商在长期生产中对全部生产要素的调整可以表现为两个方面,一方面表现为对最优的生产规模的选择,另一方面表现为进入或退出一个行业的决策。
1.1 厂商对最优生产规模的选择
在长期,厂商通过对最优生产规模的选择(调整资本\(K\)),使自己的状况得到改善,从而获得了比在短期内所能获得的更大的利润。
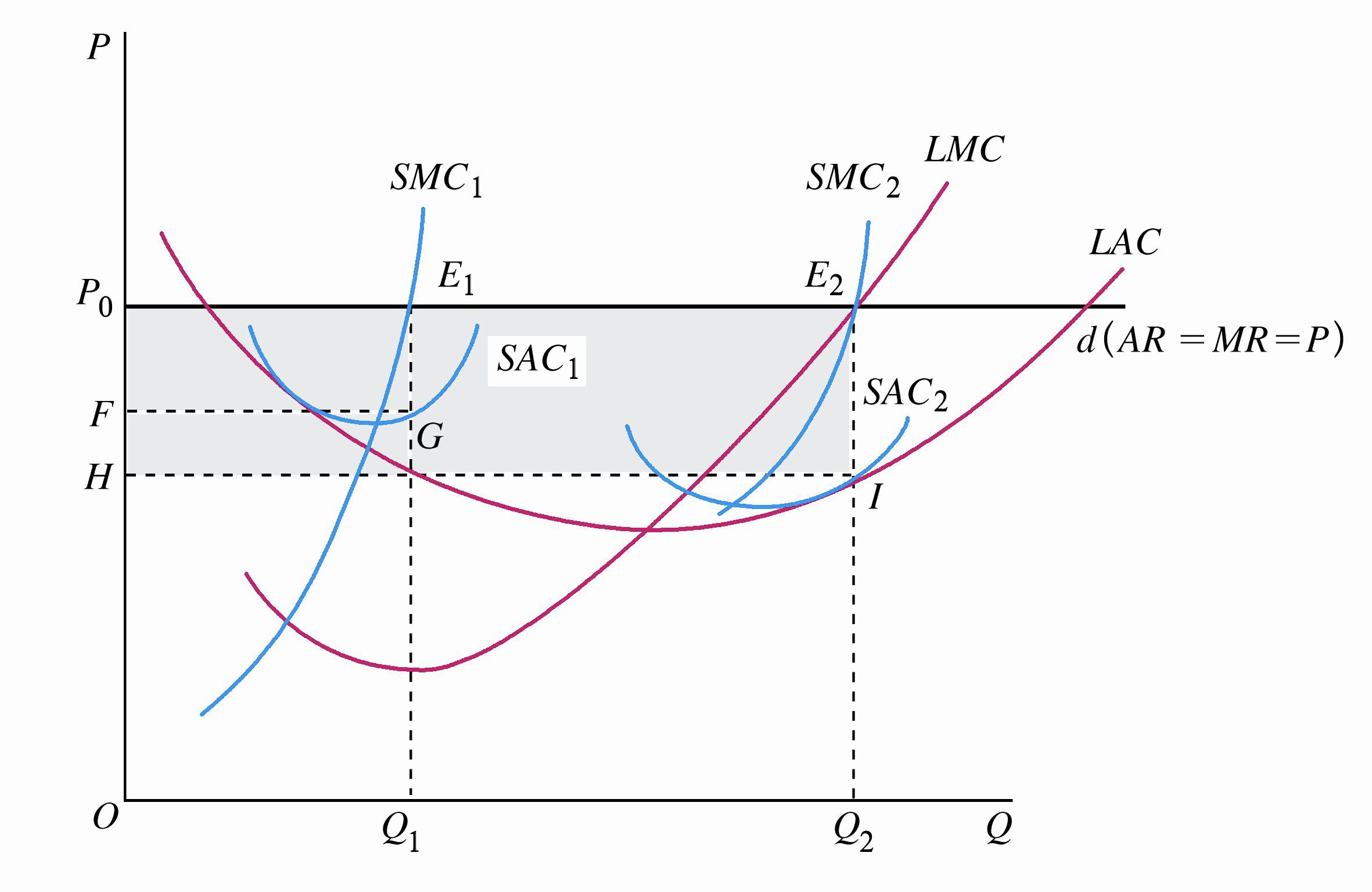
1.2 厂商进出一个行业
完全竞争厂商的长期均衡出现在 LAC 曲线的最低点。完全竞争厂商的长期均衡条件为:
\[\begin {align} MR=LMC=SMC=LAC=SAC \end {align} \]其中,\(MR=AR=P\),此时,单个厂商的利润为零。
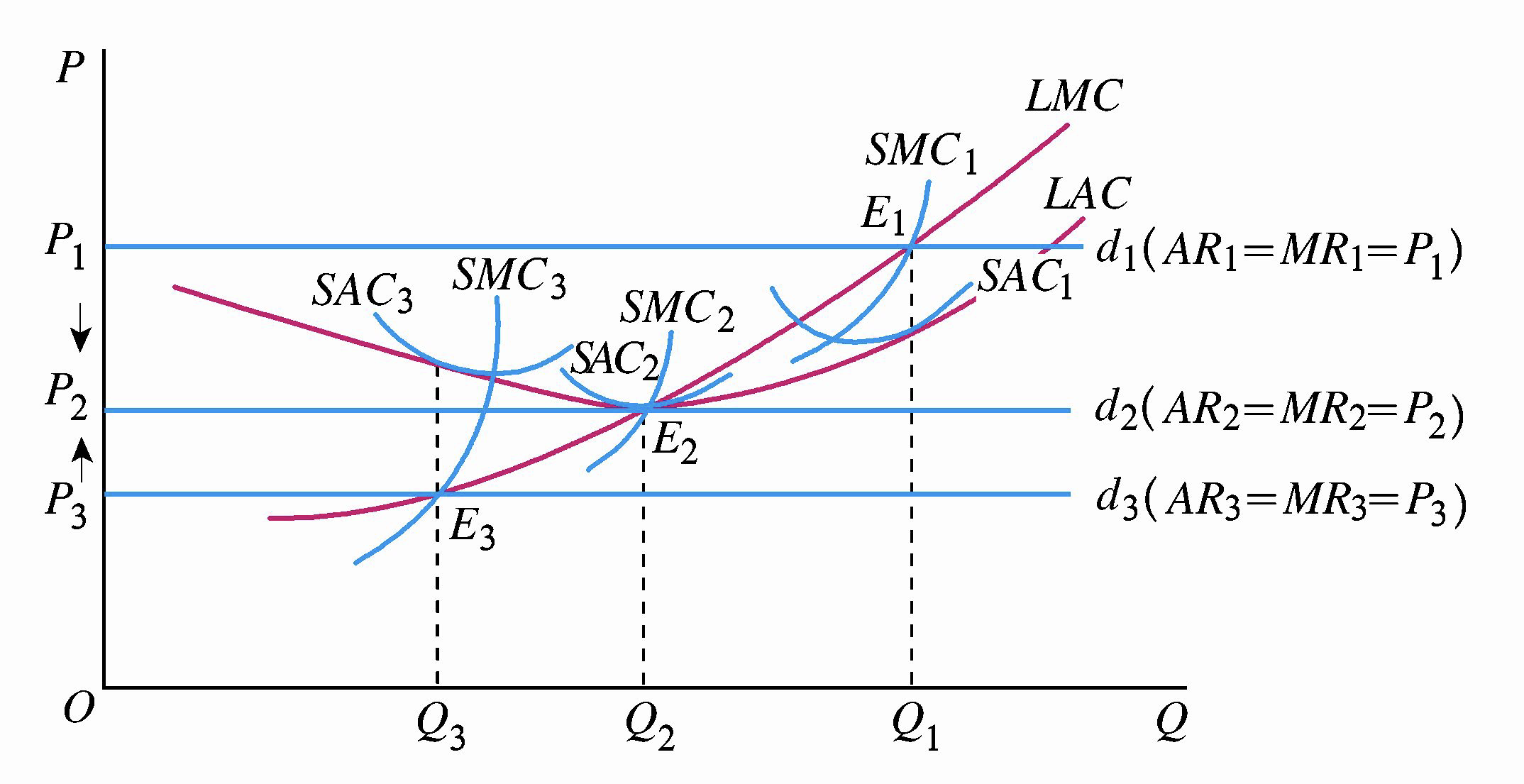
- 当价格为\(P_1\)时,由于经济利润\(\pi >0\),会有新厂商加入,市场供给量提高,会导致价格下降;
- 当价格为\(P_2\)时,由于经济利润\(\pi =0\),此时加入与退出的厂商的生产能力保持一致,供给量稳定在\(Q_2\),买个稳定在\(P_2\),为均衡状态;
- 当价格为\(P_3\)时,由于经济利润\(\pi <0\),此时,会有厂商选择退出,市场供给量下降导致价格升高。
2. 完全竞争行业的长期供给曲线
前面分析假定要素价格不变,但这种假定在长期显然不合理。当厂商进入或退出行业时,可能对市场需求产生影响,从而影响要素价格。根据行业产量变化对生产要素价格所可能产生的影响,完全竞争行业可区分为成本不变行业、成本递增行业和成本递减行业。
2.1 成本不变行业
成本不变行业是这样一种行业,该行业的产量变化所引起的生产要素需求的变化,不对生产要素的价格发生影响。成本不变行业的长期供给曲线是一条水平线,其原因在于成本不变行业的长期平均成本是不变的。
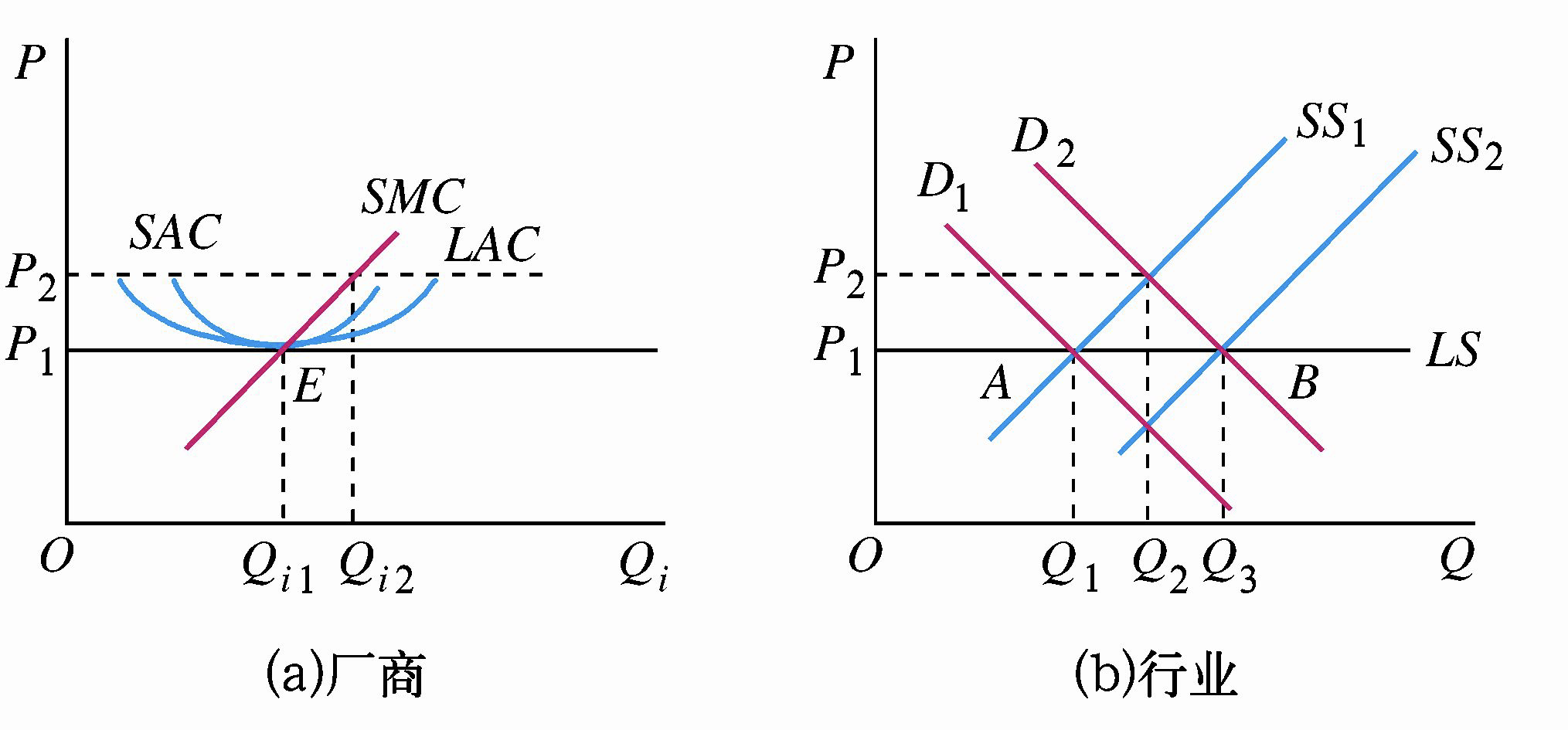
2.2 成本递增行业
成本递增行业是这样一种行业,该行业产量增加所引起的生产要素需求的增加,会导致生产要素价格的上升。成本递增行业的长期供给曲线是向右上方倾斜的,其原因在于成本递增行业的长期平均成本是递增的。
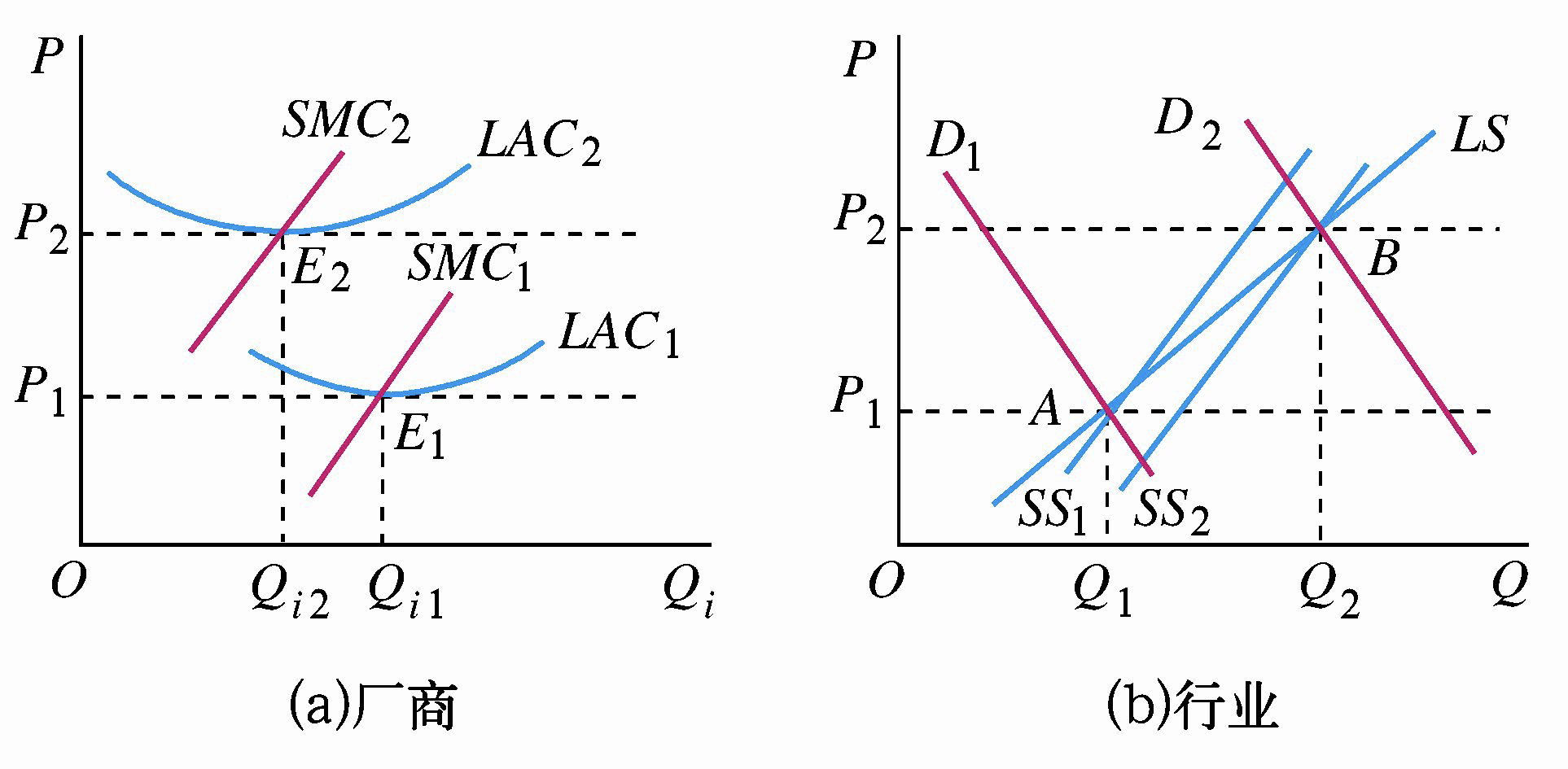
2.3 成本递减行业
成本递减行业是这样一种行业,该行业产量增加所引起的生产要素需求的增加,反而使生产要素的价格下降了。成本递减行业的长期供给曲线是向右下方倾斜的,其原因在于成本递减行业的长期平均成本是递减的。
3. 长期生产者剩余
市场的长期生产者剩余可以用市场价格线以下、行业长期供给曲线以上的部分来表示。只有在成本递增行业的长期供给曲线斜率为正的情况下,才会产生市场的长期生产者剩余。市场的长期生产者剩余也可以被理解为:要素投入者所获得的比在行业不生产时所能赚取的更高收益。

四、完全竞争市场的福利
(一)完全竞争市场的福利最大化
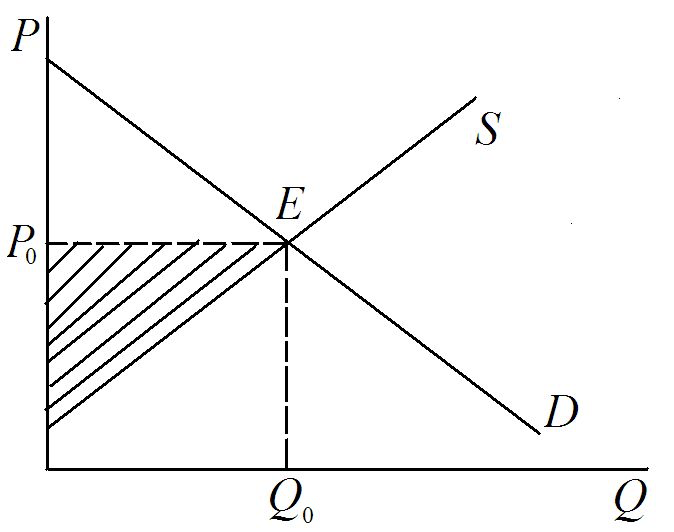
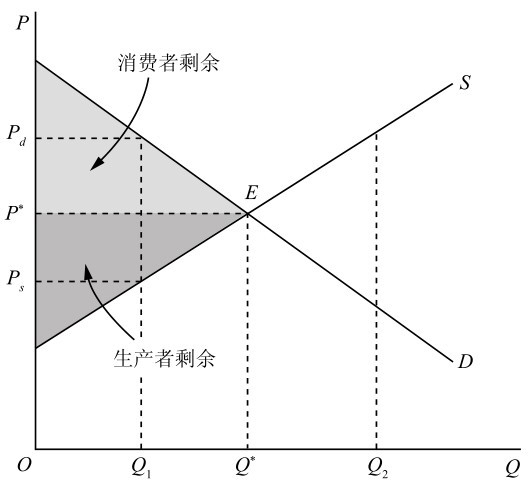
\(E\) 点是完全竞争市场的均衡点,均衡价格和均衡数量分别为 \(P^* \) 和 \(Q^* \)。如图所示,市场的消费者剩余为浅色的阴影部分面积,市场的生产者剩余为深色的阴影部分面积,市场的总剩余为消费者剩余和生产者剩余之和,实现了福利最大化。
(二)价格管制
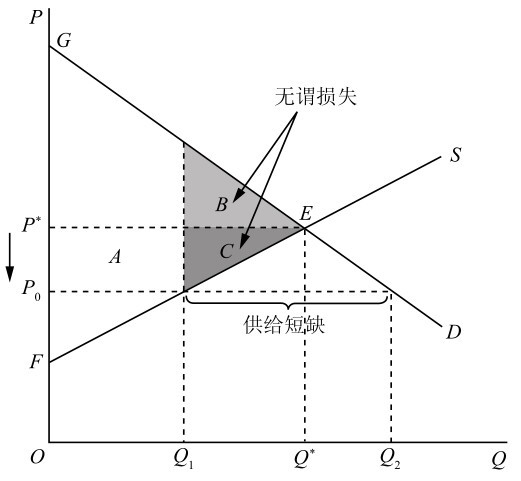
1. 最高限价
假定政府规定最高限价为 \(P_0\),由于最高限价低于均衡价格,会出现商品短缺 \(Q_2-Q_1\)。实行最高限价,市场上消费者剩余的变化量为 \(A-B\),生产者剩余的变化量为 \(-A-C\),市场总剩余损失为 \(-B -C\),此即为最高限价造成的无谓损失。(联系["限制价格"])
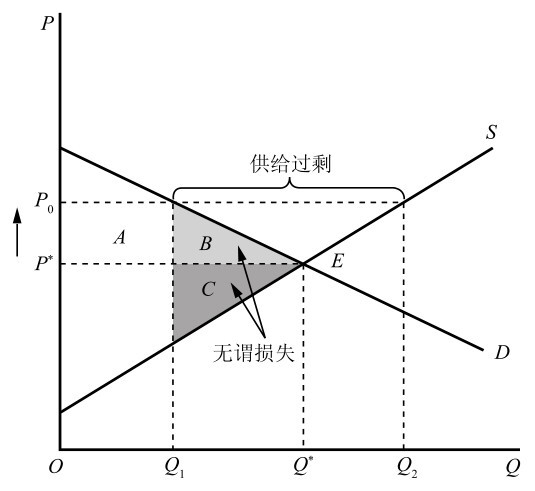
2. 最低限价
假定政府实行最低限价政策,将价格由均衡价格水平 \(P^* \) 提高到 \(P_0\)。实行最低限价,总的消费者剩余变化为 \(-A-B\),总的生产者剩余变化为 \(A-C\),因此市场总剩余的变化为 \((-A-B)+(A-C)=-B-C\),此即为最低限价造成的无谓损失。(联系["支持价格/最低限价"])
3. 销售税
3.1 政府征税
3.1.1 对厂商征税
假设政府对厂商征收税额为 \(t\) 的税,将使得厂商的生产成本增加。生产成本增加会导致供给减少,供给曲线向左移动。征税后,供给曲线由 \(S\) 左移至 \(S'\)。均衡条件为供给价格 \(P_s(Q^*)\) 加上税收 \(t\) 等于需求价格 \(P_d(Q^*)\),即:\(P_d(Q^*)=P_s(Q^*)+t\)
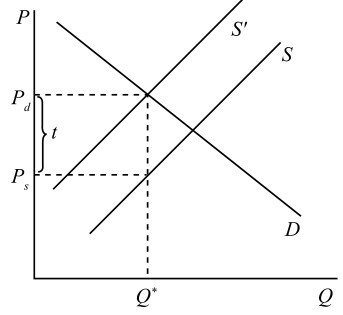
3.1.2 对消费者征税
假设政府对消费者征收税额为 \(t\) 的税,将使得消费者的实际收入(或实际购买力)下降。消费者的实际购买力下降会导致需求减少,需求曲线向左移动。征税后,需求曲线由 \(D\) 左移至 \(D'\)。均衡条件为需求价格 \(P_d(Q^*)\) 减去税收 \(t\) 等于供给价格 \(P_s(Q^*)\),即:\(P_d(Q^*)-t=P_s(Q^*)\)
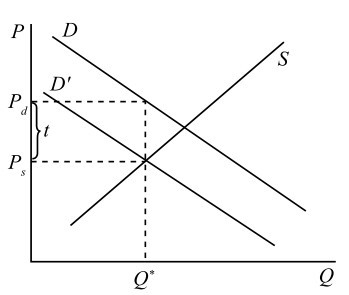
3.2 销售税的福利效应
假设政府对消费者征收 t 元的从量税,在消费者的需求曲线和生产者的供给曲线之间打进了一个垂直的“楔子”,其高度为单位商品的从量税额 t 。
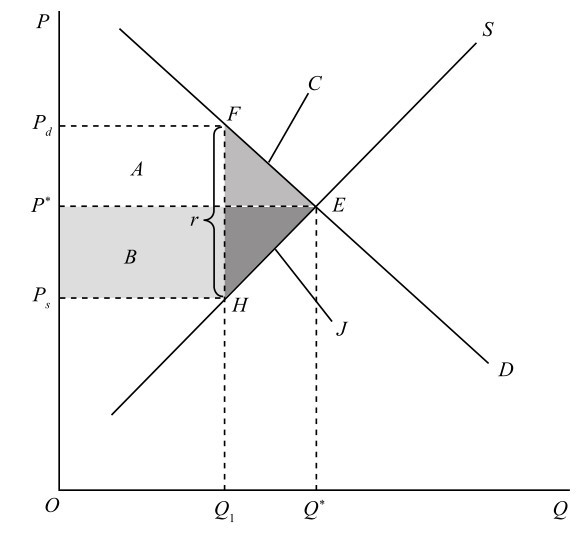
由于销售税导致的价格上升,以及需求量及供给量的减少,使得消费者剩余和生产者剩余都减少:消费者剩余的损失为 \(P_dFEP^* \) 的面积,生产者剩余的损失为 \(P_sHEP^* \) 的面积,政府获得财政收入为 \(P_dFHP_s\) 的面积,总的福利损失为 \(\Delta EFH\),此即为征税所带来的无谓损失。
3.3 销售税的税费负担
假设在完全竞争市场上,有 \(n\) 个相同的厂商与 \(m\) 个相同的消费者,且厂商生产函数与消费者需求函数均为线性函数,分别为 \(Q_s=a+bP\),\(Q_d=c-dP\)。若政府对每件商品征收 \(t\) 元的销售税,计算消费者与生产者各自承担的税费金额、政府收到的税款金额,并计算此时的消费者剩余损失、生产者剩余损失与无谓损失。
解答:市场供给曲线:\(S=nQ_s=(a+bP)n\),市场需求曲线:\(D=mQ_d=(c-dP)m\),
在征税前,市场达到均衡时 \(S=D\),可以解得:\(P^*=\frac {cm-an} {bn+dm}\)
在此价格下,厂商的产量为:\(Q_s^*= \frac {(ad+bc)m} {bn+dm}\),消费者需求量为:\(Q_d^*= \frac {(ad+bc)n} {bn+dm}\)
市场的供给量与需求量为:\(S^*=D^*=\frac {(ad+bc)nm} {bn+dm}\)
在征税后,需求价格与供给价格有 \(P_d=P_s+t\) 的关系,因此:
\[\begin {cases} Q_s=a+bP_s \\ Q_d=c-dP_d \\ P_d=P_s+t \\ nQ_s=mQ_d \\ \notag \end{cases} \]解得:\(P_s^*=\frac {cm-dmt-an} {bn+dm}\),\(P_d^*=\frac {cm+bnt-an} {bn+dm}\)
此时,厂商的产量为:\({Q'}_s^*=\frac {(ad+bc-bdt)m} {bn+dm}\),消费者需求量为:\({Q'}_d^*=\frac {(ad+bc-bdt)n} {bn+dm}\)
市场的供给量与需求量为:\({S'}^*={D'}^*=\frac {(ad+bc-bdt)nm} {bn+dm}\)
消费者的税费负担为:\(P_d^*-P^*=\frac {bnt} {bn+dm}\)
生产者的税费负担为:\(P^*-P_s^*=\frac {dmt} {bn+dm}\)
此时,消费者剩余损失、生产者剩余损失的几何形状为梯形:
市场的消费者剩余损失为:\(\frac {({S'}^*+S^*) \times (P_d^*-P^*)} 2=\frac {(2ad+2bc-bdt)bn^2mt} {2(bn+dm)^2}\)
市场的生产者剩余损失为:\(\frac {({S'}^*+S^*) \times (P^*-P_s^*)} 2=\frac {(2ad+2bc-bdt)dnm^2t} {2(bn+dm)^2}\)
政府税收为:\((P_d-P_s){S'}^*=t \times {S'}^*=\frac {(ad+bc-bdt)nmt} {bn+dm}\)
无谓损失为:\(\frac {t(S^*-{S'}^*)} 2=\frac {bdnmt^2} {2(bn+dm)}\)
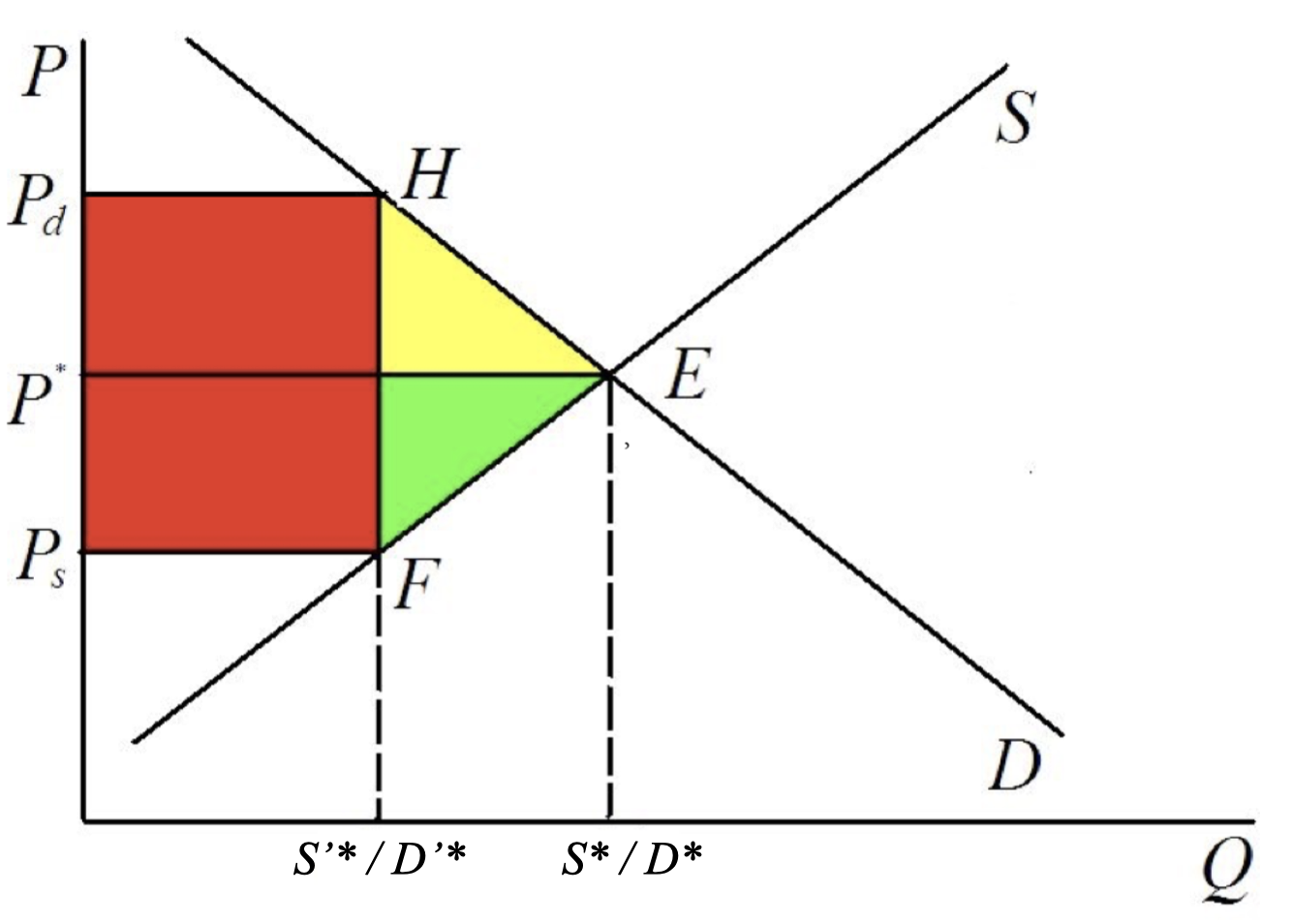
思路补充:
- 绘制示意图
- 计算未征税时的市场均衡价格\(P^* \)、商品量\(Q^* \)
- 计算征收后的供给量\(Q_s\)、需求量\(Q_d\)、供给价格\(P_s\)、需求价格\(P_d\)
- 基于示意图,计算生产者剩余与消费者剩余的损失,计算无谓损失。
向消费者征收消费税与所得税
向消费者征收相同的税收,征收所得税比征收消费税更优。
分析过程:
假设初始预算约束为:
\[\begin{align} p_1x_1+p_2x_2=m \end {align} \]按照税率\(t\)对商品1进行征税,相当于商品1的价格上涨了\(t\)。此时新的预算约束为:
\[\begin{align} (p_1+t) x_1^*+p_2 x_2^*=m \end {align} \]通过征税,政府收入增加\(R^* = t x_1^* \)
如果政府征收相同的所得税,此时预算约束为:
\[\begin{align} p_1x_1+p_2x_2= m - R^* = m-t x_1^* \end {align} \]
如上图所示,征收所得税的预算约束线斜率与不征税时的预算约束线斜率相同,且经过点\((x_1^*,x_2^*)\),在该点处的边际替代率为\(-\frac {(p_1+t)} {p_2}\)。
在征收所得税时,在该点处边际替代率为\(-\frac {p_1} {p_2}\),预算约束线与无差异曲线相交于点\((x_1^*,x_2^*)\),因此预算约束线上存在一些点比点\((x_1^*,x_2^*)\)处更受到消费者的偏好。