一、垄断市场
(一)定义与形成的原因
1. 定义
垄断市场是指整个行业中只有唯一的一个厂商的市场组织。垄断厂商可以控制和操纵市场价格。
2. 结构特征:
- 单个生产者:市场上只有唯一的一个厂商生产和销售商品;
- 无替代品:该厂商生产和销售的商品没有任何相近的替代品;
- 不存在潜在竞争者:其他任何厂商进入该行业都极为困难或不可能;
- 可以决定价格:垄断地位的经济主体是市场价格的制定者,它能够自行决定价格,以实现自己的利润最大化;
- 可以差别定价:垄断企业为实现利润最大化,可以在不同的销售条件下对产品制定不同的价格。
3. 垄断形成的原因
- 独家厂商控制了生产某种商品的全部资源或基本资源供给;
- 独家厂商拥有生产某种商品的专利权;
- 政府的特许;
- 自然垄断:某些产品或服务由单个企业大规模生产经营,比多个企业同时生产经营更有效率。
(二)均衡条件
1. 需求曲线与收益曲线
(比较完全竞争厂商的["需求曲线"]与["收益曲线"])
厂商的平均收益曲线与需求曲线重叠,它们是同一条向右下方倾斜的曲线。这表明垄断厂商的销售量与市场价格呈反方向变动关系,垄断厂商可以通过改变销售量来控制市场价格。
厂商的边际收益曲线向右下方倾斜,且位于平均收益曲线的下方,这表示在每一个销售量上厂商的边际收益都小于平均收益。
厂商的总收益曲线是先上升,达到最高点以后再下降。
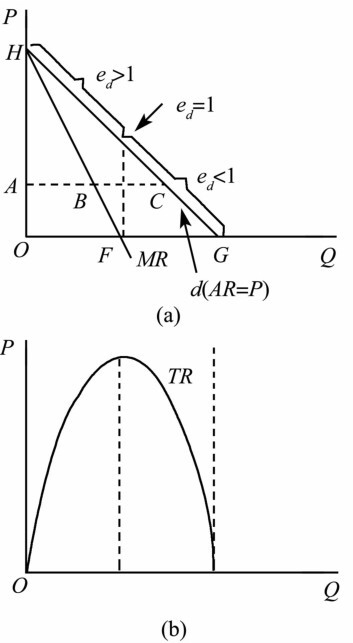
2. 需求价格弹性
假定反需求函数为 \(P=P(Q)\),则有:\(MR=\frac {dTR(Q)} {dQ}=P+\frac {dP} {dQ}\cdot Q=P \Big (1-\frac 1 {e_d} \Big)\)
补充:
- ["需求价格弹性"]:\(e_d= - \frac {d Q_d} {d P} \times \frac P {Q_d}\)
因此,在垄断市场中,可得以下三种情况:
- 当 \(e_d>1\) 时,有 \(MR>0\),增加产量可以提高总收益 \(TR\);
- 当 \(e_d<1\) 时,有 \(MR<0\),减少产量可以提高总收益 \(TR\);
- 当 \(e_d=1\) 时,有 \(MR=0\),总收益 \(TR\) 达到最大。
3. 垄断厂商的均衡
补充:
短期内,垄断厂商的经营决策依据:
- 确定产量与价格:\(MR\) 与 \(MC\) 比较
- 是否盈利:\(AR\) 与 \(AC\) 比较
3.1 利润最大化的图形分析
垄断厂商为了获得最大的利润,也必须遵循 \(MR = MC\) 的原则,即 \(MC=MR=P \big (1-\frac 1 {e_d} \big)\),
- 垄断厂商利润最大化的选择不可能出现在需求缺乏弹性的区域,只可能出现在需求富有弹性的地方。
- 由于 \(MR=P(q) \big (1-\frac 1 {e_d} \big)\),只要 \(e_d<\infty\),则 \(MR<P(q)\),即边际收益总会小于价格,对应的边际收益曲线总是处于平均收益曲线的下方。
3.2 短期均衡
与["完全竞争厂商"]类似,在短期均衡时,垄断厂商由 \(MC=MR\) 确定产量,由平均成本 \(AC\) 与平均收益 \(AR\)(\(P=AR\))的大小比较确定是否盈利或亏损。
补充:
["完全竞争市场"]: \(MR=P\),因为完全竞争厂商是价格接受者,\(P\)与该厂商的产量无关,\(MR=\frac {\partial TR } {\partial Q} =\frac {\partial (P \cdot Q) } {\partial Q} = P\)
垄断竞争市场: \(MR=P \big (1-\frac 1 {e_d} \big)\),垄断厂商可以通过调整产量来操控价格,因此价格是产量的函数\(P(Q)\),\(MR=\frac {\partial TR } {\partial Q} =\frac {\partial (P \cdot Q) } {\partial Q} = P+\frac {\partial P } {\partial Q} \cdot Q = P \big (1-\frac 1 {e_d} \big)\)
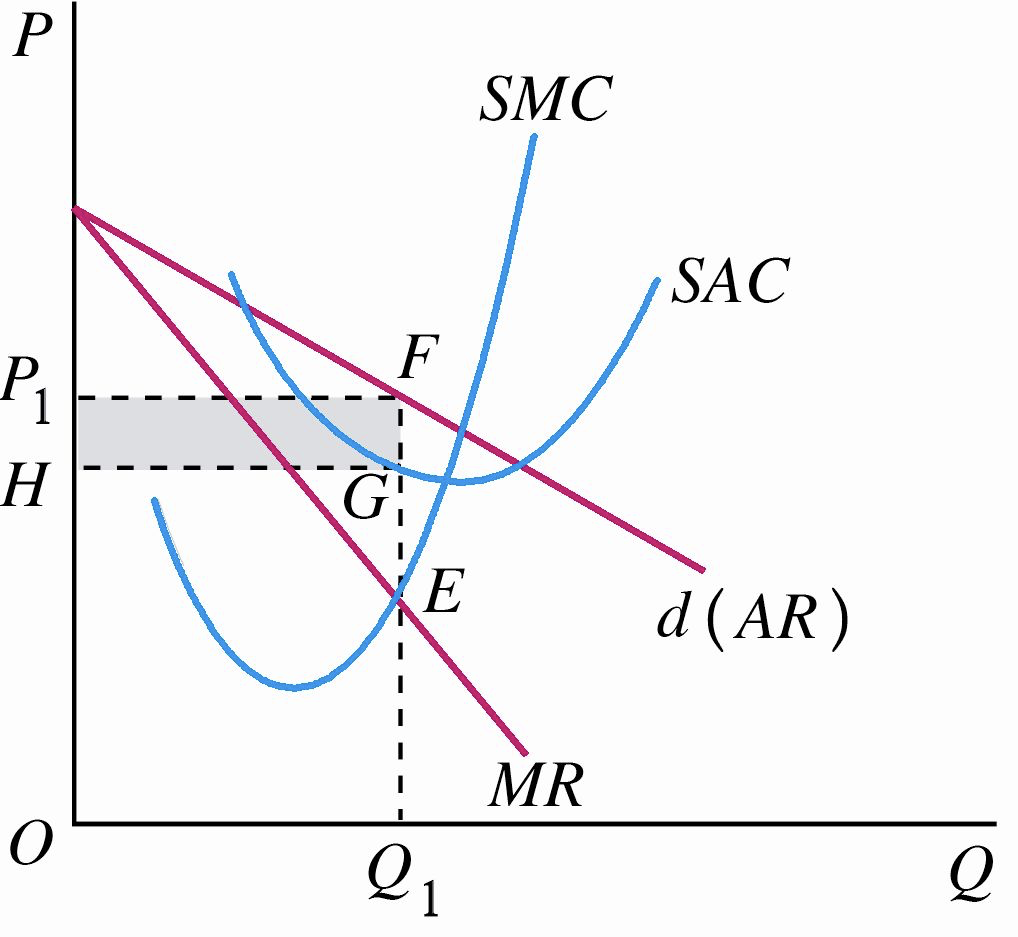
3.2.1 盈利
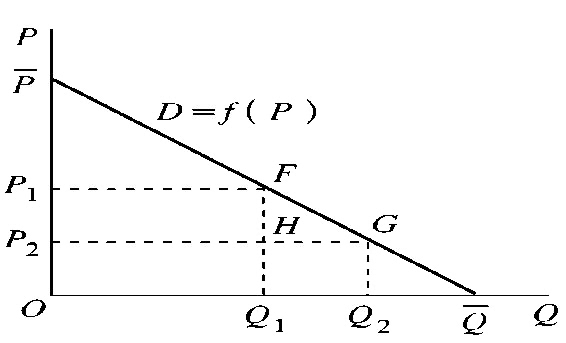
如图所示,垄断厂商获得利润,总利润量矩形 \(P_1FGH\) 的面积。
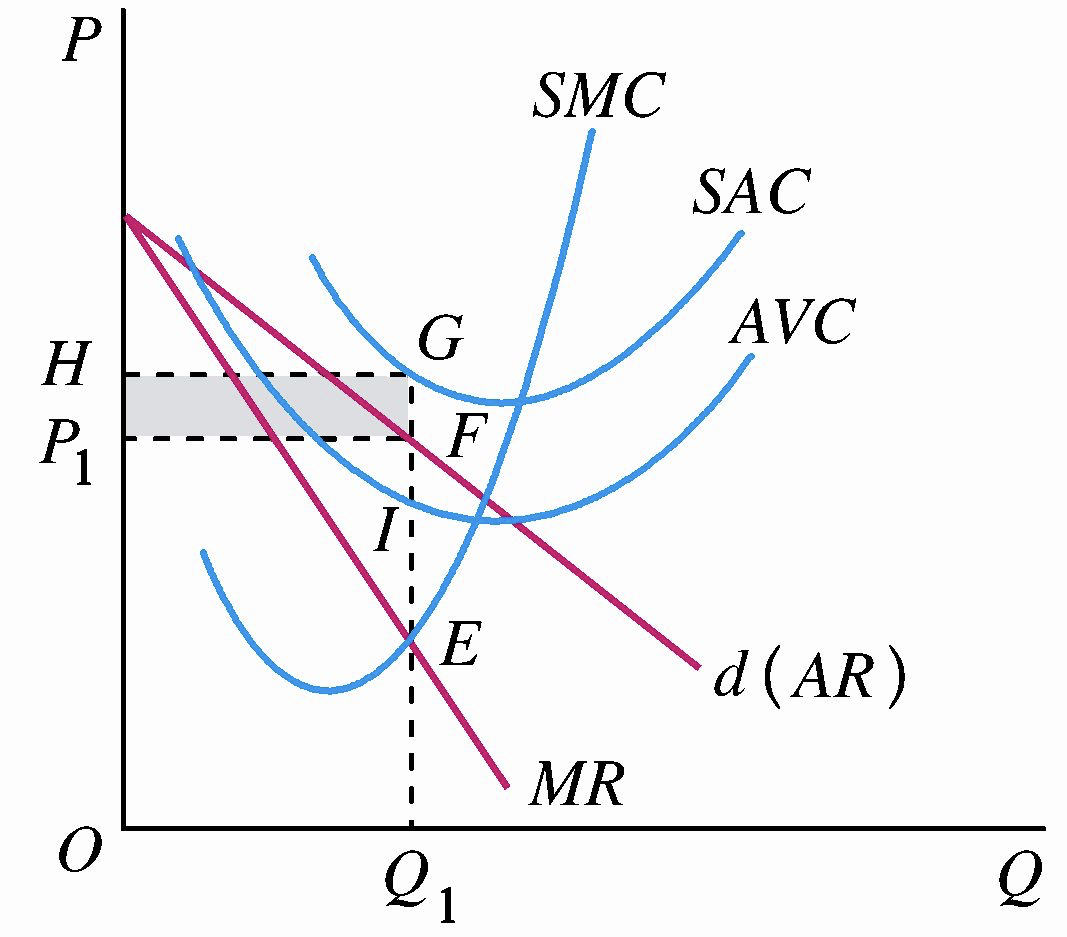
3.2.2 亏损
垄断厂商在短期内由于不能调整生产规模,并非总能获得利润。如图所示,垄断厂商是亏损的,亏损额相当于矩形 \(P_1FGH\) 的面积。
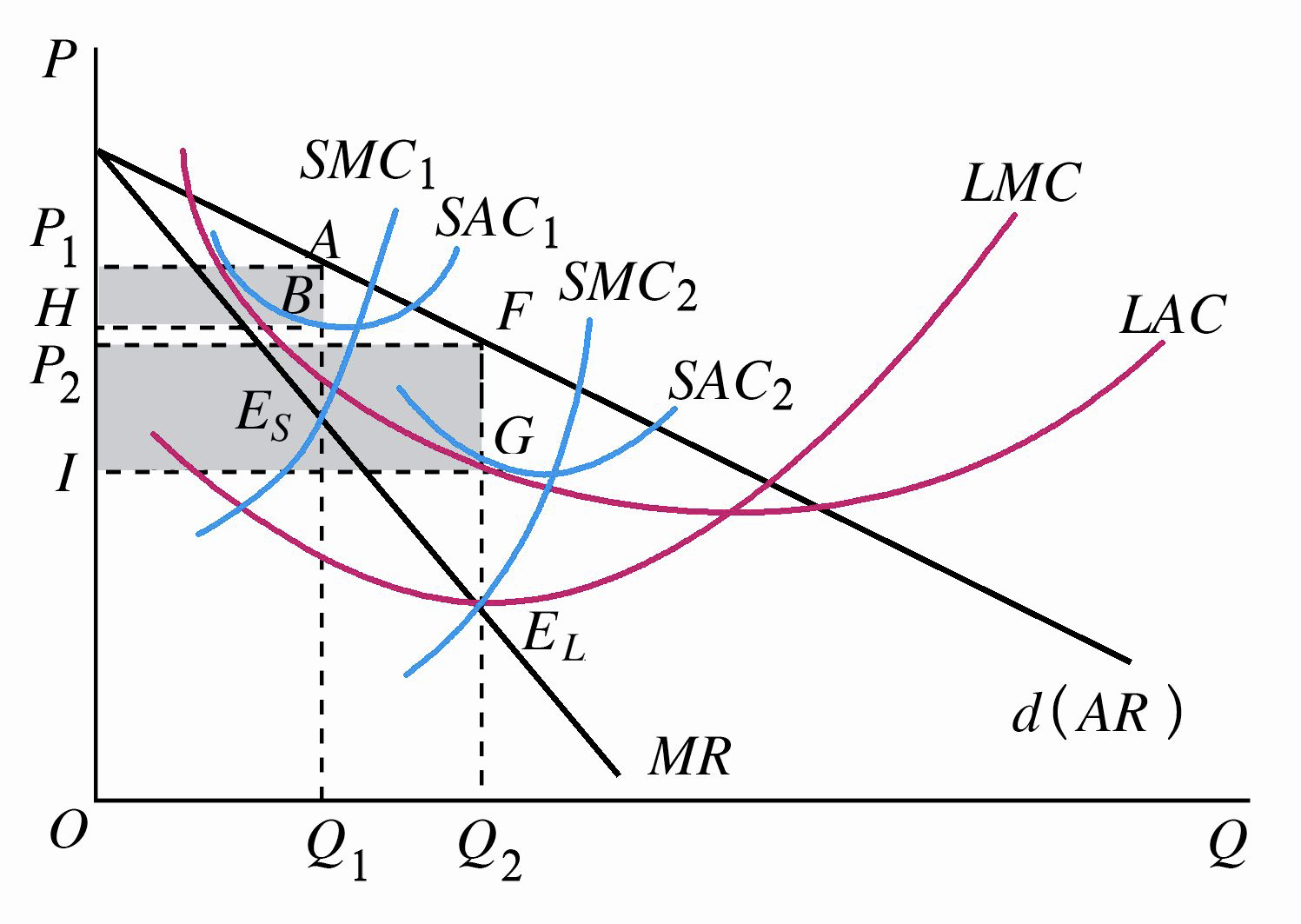
3.3 长期均衡的条件
垄断厂商长期均衡的条件为:\(MR=LMC=SMC\)
垄断厂商之所以能在长期内获得更大的利润,其原因在于长期内企业的生产规模是可调整的,而且市场对新加入厂商是完全关闭的。
垄断厂商对生产调节的结果:
- 垄断商场在短期内亏损,且在长期不存在一个可以使之获得利润(或至少使亏损为 0)的最优生产规模,那么该厂商将退出生产。
- 垄断厂商在短期内亏损,但在长期内通过对最优生产规模的选择,摆脱亏损状况,甚至获得利润,此时厂商不退出生产。
- 垄断厂商在短期内利用既定生产规模获得了利润,在长期通过对生产规模调整,使自己获得更大的利润,此时厂商不退出生产。
3.4 供给曲线
供给曲线表示在每一个价格水平生产者愿意而且能够提供的产品的数量,体现了产量和价格之间的一一对应关系。但是垄断厂商可以通过产量和价格的同时调整来实现利润最大化,所以垄断厂商的价格和产量之间不再必然存在一一对应的关系。(对比["完全竞争市场的长期供给曲线"])
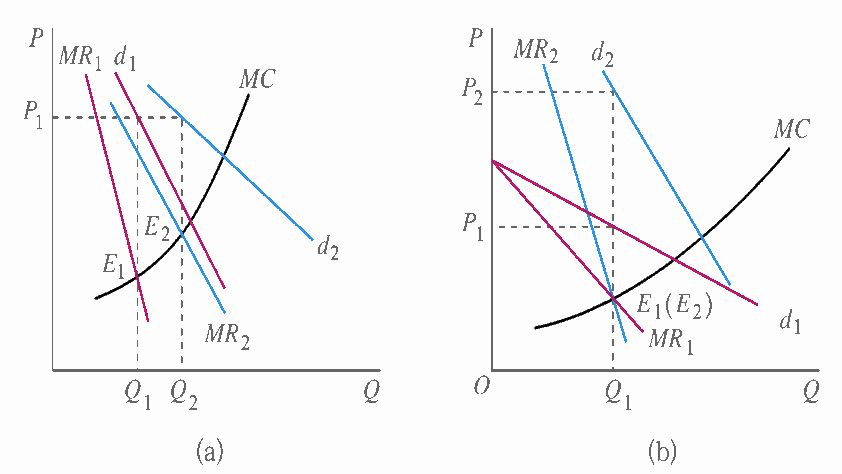
垄断厂商没有供给曲线,即无法得到如同完全竞争市场条件下的具有规律性的、可以表示产量与价格一一对应的短期供给曲线。
==凡是在或多或少的程度上带有垄断因素的不完全竞争市场中(单个厂商对市场价格有一定的控制力量),即在单个厂商的需求曲线向右下方倾斜的市场中,不存在具有规律性厂商和行业的短期和长期供给曲线。==
(三)价格歧视
**以不同价格销售同一种产品,被称为价格歧视。**价格歧视不只存在于垄断厂商,凡是厂商对其产品市场具有价格影响力或控制力者皆可采取价格歧视。
价格歧视要可行,必须满足两个基本条件:
- 第一,市场的消费者具有不同的偏好,且这些不同的偏好可以被区分开;
- 第二,不同的消费者群体或不同的销售市场是相互隔离的。
1. 一级价格歧视
一级价格歧视 / 完全价格歧视(perfect price discrimination), 指厂商对每一单位产品都按消费者所愿意支付的最高价格出售(每一单位的产品价格都不相同)。
如图所示,当消费者欲购买 \(q_0\) 的数量时,其实际支出的金额为 \(Oq_0BA\),恰好等于其所愿意支出的最大金额。
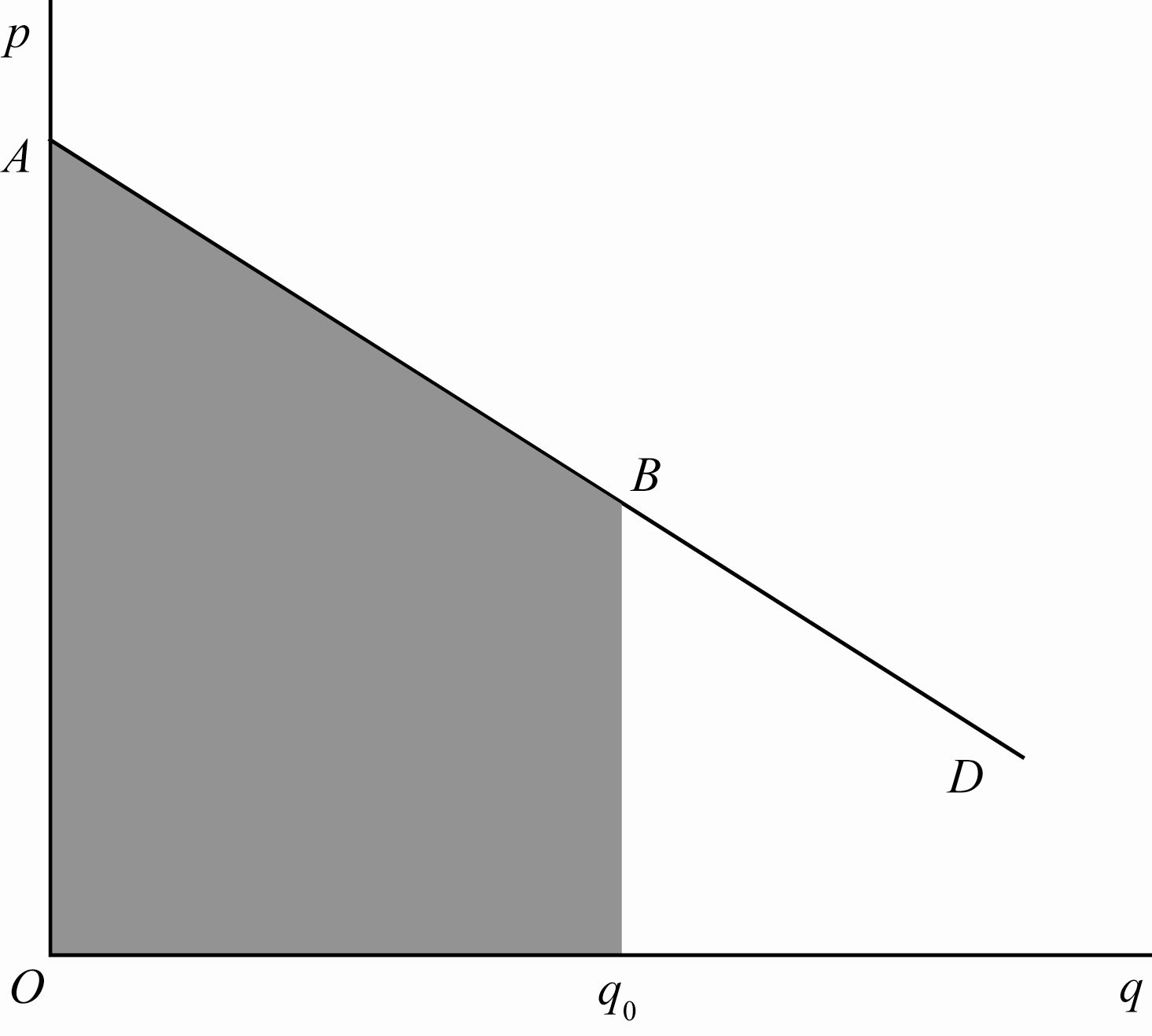
一级价格歧视是一种罕见的价格歧视情况。实际上,只有当垄断厂商确切了解每个消费者对其产品的需求曲线时,一级价格歧视才可能发生。
实行一级价格歧视的垄断厂商,可以榨取所有的消费者剩余(\(CS=0\))。
2. 二级价格歧视(数量歧视)
二级价格歧视 / 非线性定价(non linear pricing),是指厂商对不同的消费数量段规定不同的价格。购买相同数量的消费者支付相同的价格,不同消费数量之间存在价格歧视。
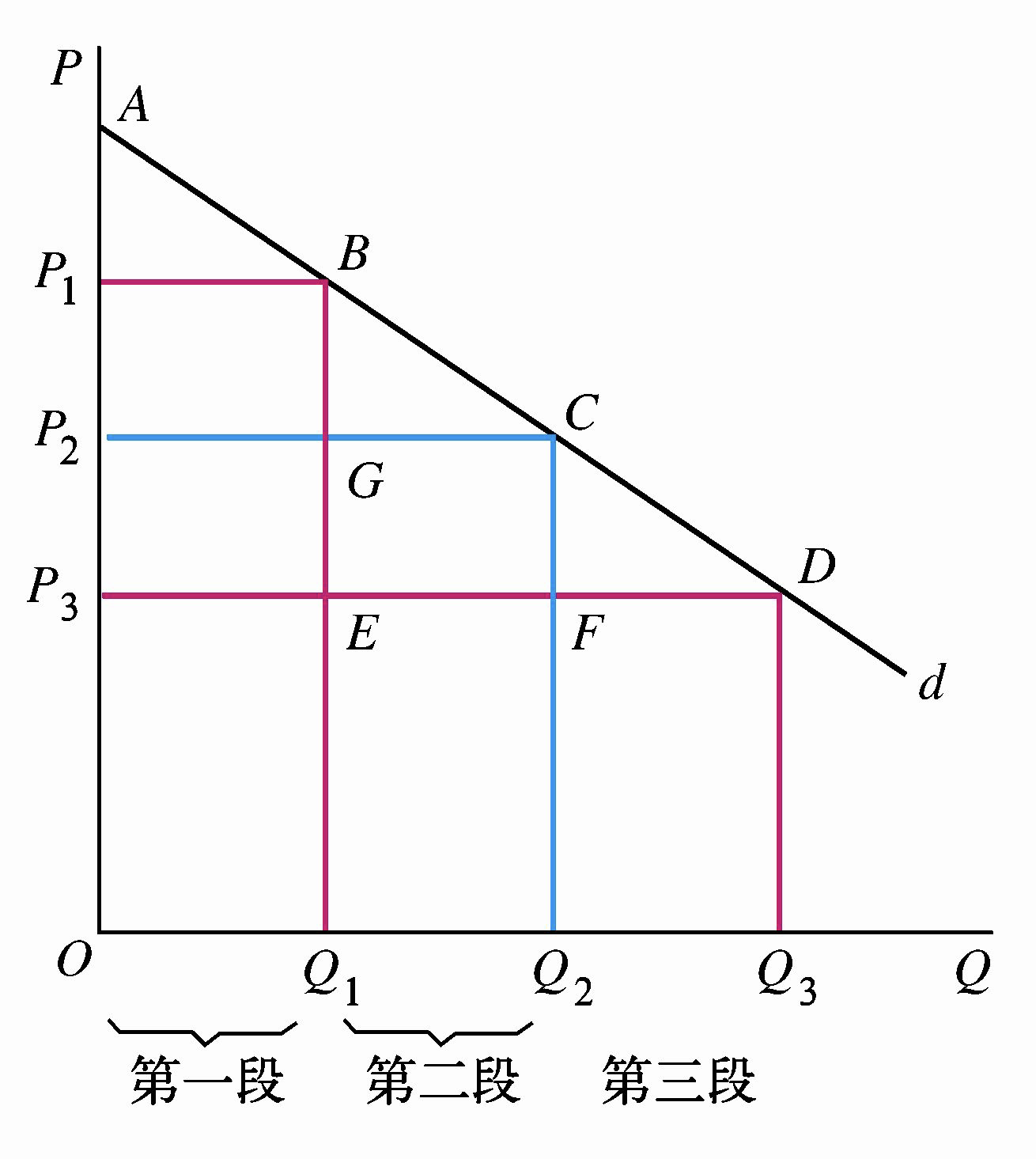
实行二级价格歧视的垄断厂商利润会增加,部分消费者剩余被垄断者占有,且垄断者会达到或接近 \(P =MC\) 的有效率的资源配置的产量。
二级价格歧视更多用于社会公用事业中,其产品必须是易于度量与记录并且成批出售。
一级价格歧视与二级价格歧视的区别:
- 一级价格歧视实质是逐个出售,二级价格歧视是分批定价、分批出售;
- 一级价格歧视对每个消费者收取不同的价格,二级价格歧视的价目表面对所有买主。
3. 三级价格歧视
三级价格歧视是指厂商对同一种产品在不同的市场上(或对不同的消费群)收取不同的价格。
实施三级价格歧视,需要满足 2 个条件:
- 垄断厂商能对不同的消费者进行有效隔离
- 消费者的自我选择
举例:
- 富人区和贫民区的价格不同(地域因素)
- 学生于非学生价格不同(身份因素)
- 黄金时间段和非黄金时间段收费不同(时间因素)
三级价格歧视的特点:
- 产量决策原则:\(MR_1=MR_2=MC\),垄断商场根据 \(MC=MR\) 确定产量水平,主要根据地理差别、产品用途、时间、消费者收入等将同一产品分配在不同的市场上。
- 价格决策原则:需求价格弹性 \(e_d\) 小的市场价格高,需求价格弹性 \(e_d\) 大的市场价格低;
- 三级价格歧视的利润高于统一定价。
证明过程补充:
假设存在两个不同的市场(或两种不同的消费人群),厂商采取三级价格歧视,即对两个市场采取区别定价,因此两个市场的因此边际收益 \(MR\) 不同,但提供的产品相同,边际成本 \(MC\) 相同,此时垄断厂商利润最大化的条件为:\(MR_1=MR_2=MC\)
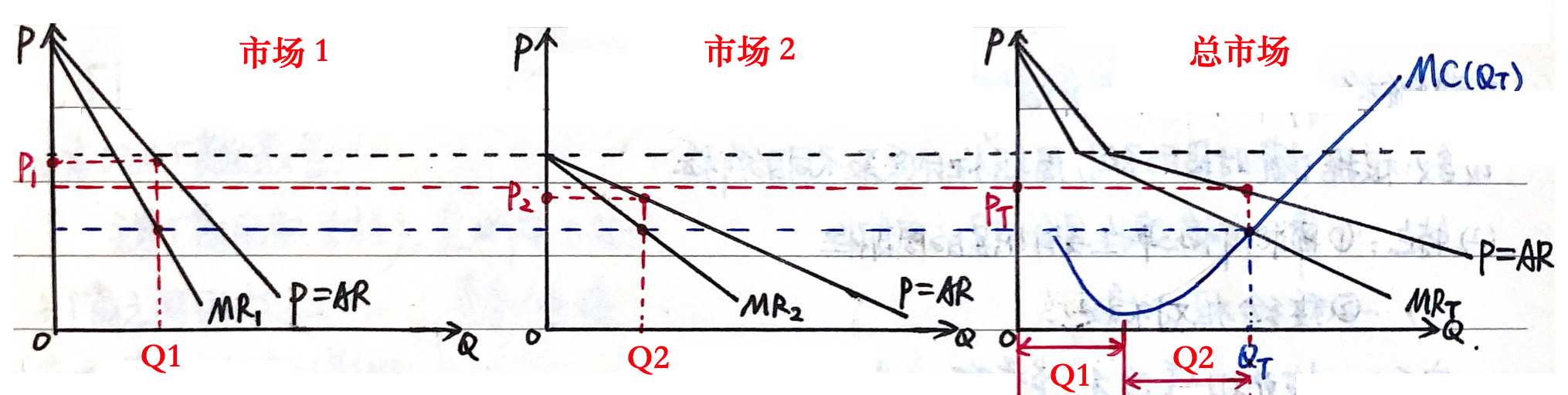
在两个市场中,分别有:
\(\begin {align} MR_1 = P_1 \Big (1-\frac 1 {e_{d,1}} \Big) \\ MR_2 = P_2 \Big (1-\frac 1 {e_{d,2}} \Big) \end {align}\)
因此,根据厂商利润最大化条件 \(MC = MR_1 = MR_2\),可以计算出:
\(\begin {align} \frac {P_1} {P_2}=\frac {1- 1 /{e_{d,2}}} {1- 1 /{e_{d,1}}} \end {align}\)
4. 小结

5. 垄断厂商其他定价策略
5.1 两部收费制
对一种商品或服务收取两次价格(入门费 + 使用费)。
特点:
- 剥夺消费者剩余
- 利润取决于使用费和入门费
- 适用于消费需求近似的商品
例如:园中园收费、会员制收费、固定电话收取月租费
5.2 时期间价格歧视
根据销售的不同时间收取不同的价格(三级价格歧视的一种)。
特点:
- 用时间作为区分消费者的手段
- 根据弹性不同定价
例如:季节性打折、电影放映的定价
5.3 高峰价格
根据消费时段不同,周期性地采取不同的价格。
特点:
- 需求价格弹性具有明显的周期性
- 供给相对稳定
例如:旅游旺季价与淡季价、用电分时定价
5.4 搭售
两种或更多商品作为一组商品定价。
特点:
- 剥夺消费者剩余
- 适用于消费上负相关的商品
- 纯搭售与混合搭售
例如:快餐套餐、有线电视频道组合
二、垄断竞争市场
(一)概念与形成条件
垄断竞争市场:一个市场中有许多厂商生产和销售有差别的同种产品的市场组织(垄断竞争:monopolistic competition)。
生产集团:市场上大量的生产非常接近的同种产品的厂商的总和。
垄断竞争市场的条件:
- 在生产集团中有大量的企业生产有差别的同种产品,这些产品彼此之间都是非常接近的替代品(如:不同品牌的香烟、方便面、饮料);
- 一个生产集团中的企业数量非常多,以至于每个厂商都认为自己的行为的影响很小,不会引起竞争对手的注意和反应,因而自己也不会受到竞争对手的任何报复措施的影响(如:盒饭、理发业);
- 厂商的生产规模比较小,进入和退出一个生产集团比较容易(如:轻工业、修理业、零售业)。
(二)需求曲线
1. 需求曲线的形状
由于垄断竞争厂商可以在一定程度上控制自己产品的价格,垄断竞争厂商所面临的需求曲线也是向右下方倾斜的。市场中的竞争因素又使得垄断竞争厂商面临的需求曲线具有较大的弹性。因此,垄断竞争厂商向右下方倾斜的需求曲线是比较平坦的,相对地比较接近["完全竞争厂商的水平形状需求曲线"]。
2. 需求曲线的种类
**主观需求曲线 **/ \(dd\) 需求曲线:在垄断竞争生产集团中的某个厂商改变产品价格,而其他厂商的产品价格都保持不变时,该厂商的产品价格和销售量之间的关系。
**客观需求曲线 **/ \(DD\) 需求曲线:在垄断竞争生产集团的某个厂商改变产品价格,而且集团内的其他所有厂商也使产品价格发生相同变化时,该厂商的产品价格和销售量之间的关系。
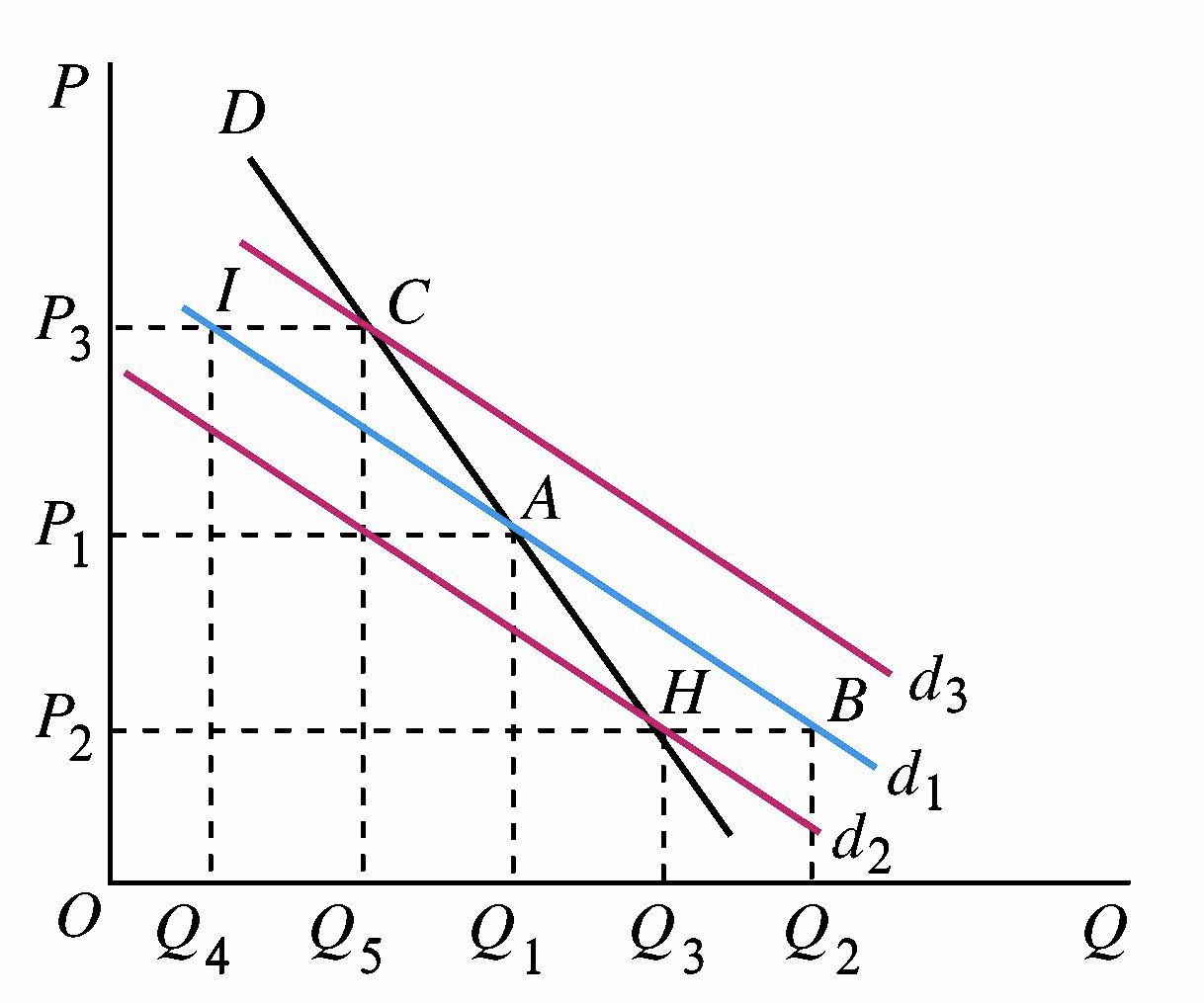
主观需求曲线和客观需求曲线的关系:
- 当垄断竞争生产集团内的所有厂商都以相同方式改变产品价格时,整个市场价格的变化会使得单个垄断竞争厂商的主观需求曲线的位置沿着客观需求曲线上下平移。如果市场价格下跌,则主观需求曲线沿着客观需求曲线向下平移,如果市场价格上升,则主观需求曲线沿着客观需求曲线向上平移。
- 由于主观需求曲线表示单个垄断竞争厂商单独改变价格时所预期的产量,客观需求曲线表示每个垄断竞争厂商在每一市场价格水平实际面临的市场需求量,因此,主观需求曲线和客观需求曲线相交意味着垄断竞争市场的供求相等状态。
- 主观需求曲线的弹性大于客观需求曲线,即主观需求曲线更加平坦。
(三)短期均衡与长期均衡
1. 短期均衡
在短期内,垄断竞争厂商是在现有的生产规模下通过对产量和价格的调整,来实现 \(MR=SMC\) 的均衡条件。在短期均衡的产量上,一定存在着一个主观需求曲线和客观需求曲线的交点,这意味着市场上的供求是相等的。同样在短期均衡时,垄断竞争性厂商可能获得最大的利润,也可能利润为零,也可能蒙受最小损失。
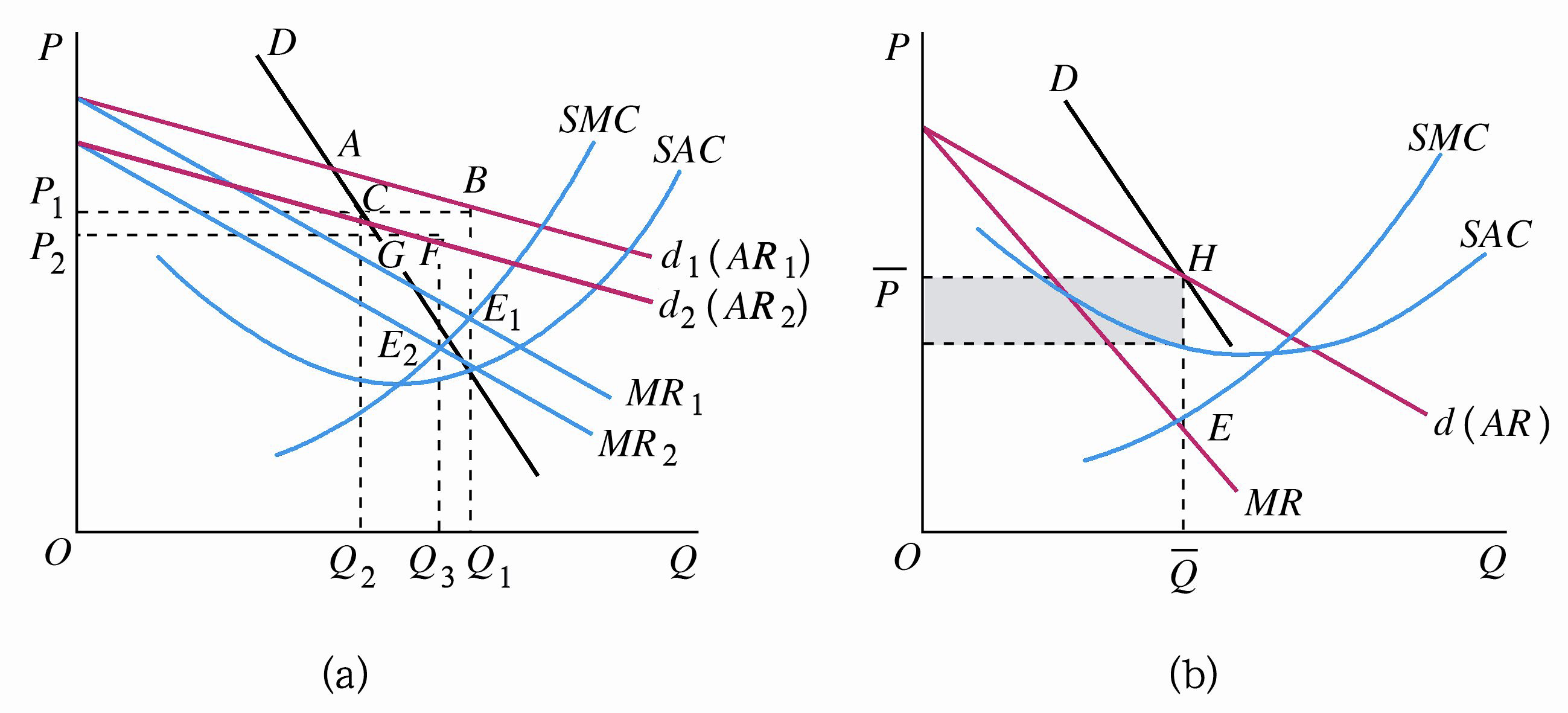
主观需求曲线和客观需求曲线相交点对应的产量和价格恰好是 \(MR=SMC\) 时的均衡点 \(E\) 所要求的产量和价格。此时,企业便实现了短期均衡。
2. 长期均衡
垄断竞争厂商的长期均衡条件为:\(MR=LMC=SMC\),\(AR=LAC=SAC\),即边际收益等于边际成本,平均收益等于平均成本。这一条件表明:垄断竞争厂商在长期均衡时的利润必定为零,即在垄断竞争厂商的长期均衡点上,主观需求曲线必定与 \(LAC\) 曲线相切。
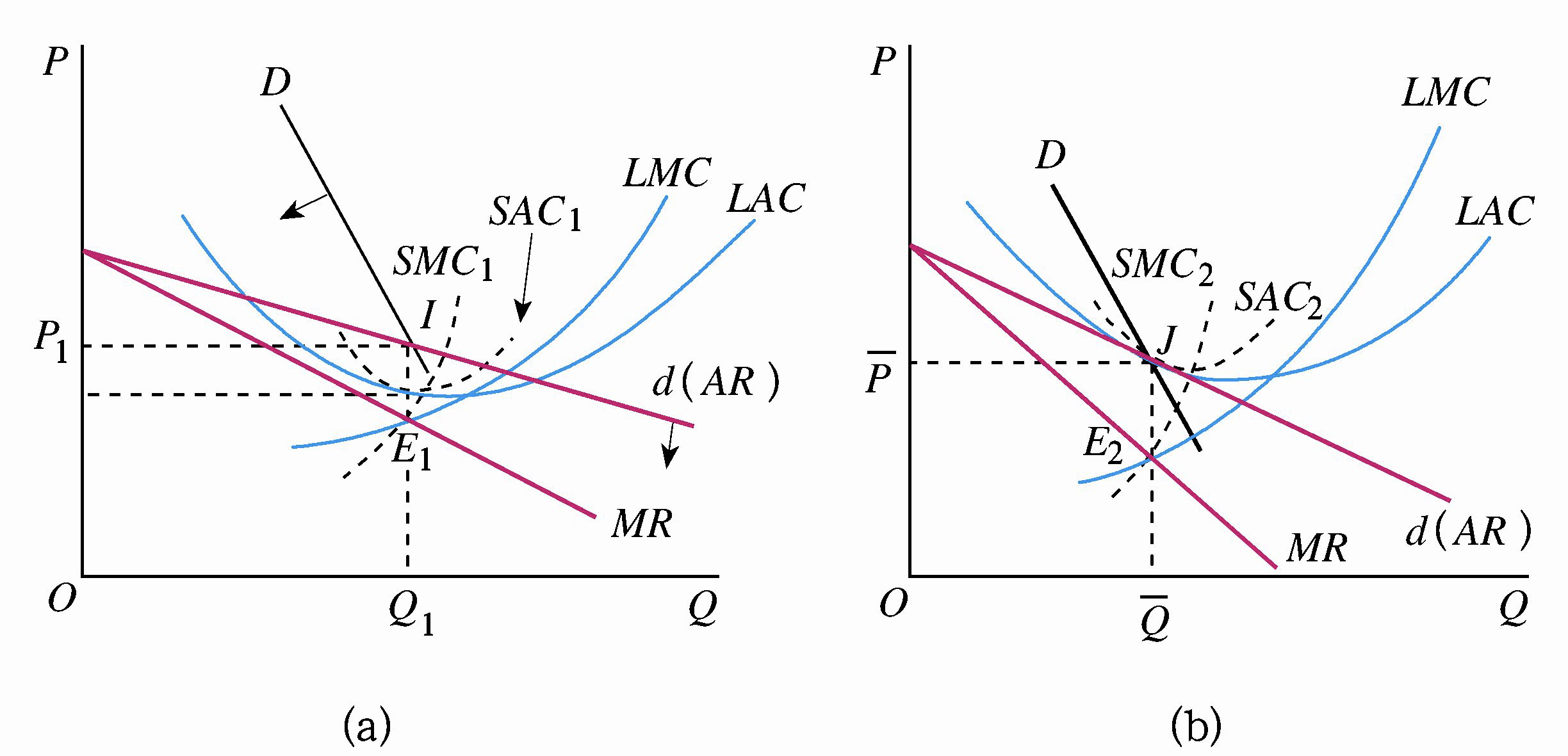
(四)效率损失与非价格竞争
1. 垄断竞争的效率损失:多余生产能力
一般把完全竞争企业在长期平均成本 \(LAC\) 曲线最低点上的产量称作理想的产量,把实际产量与理想产量之间的差额称作多余的生产能力。
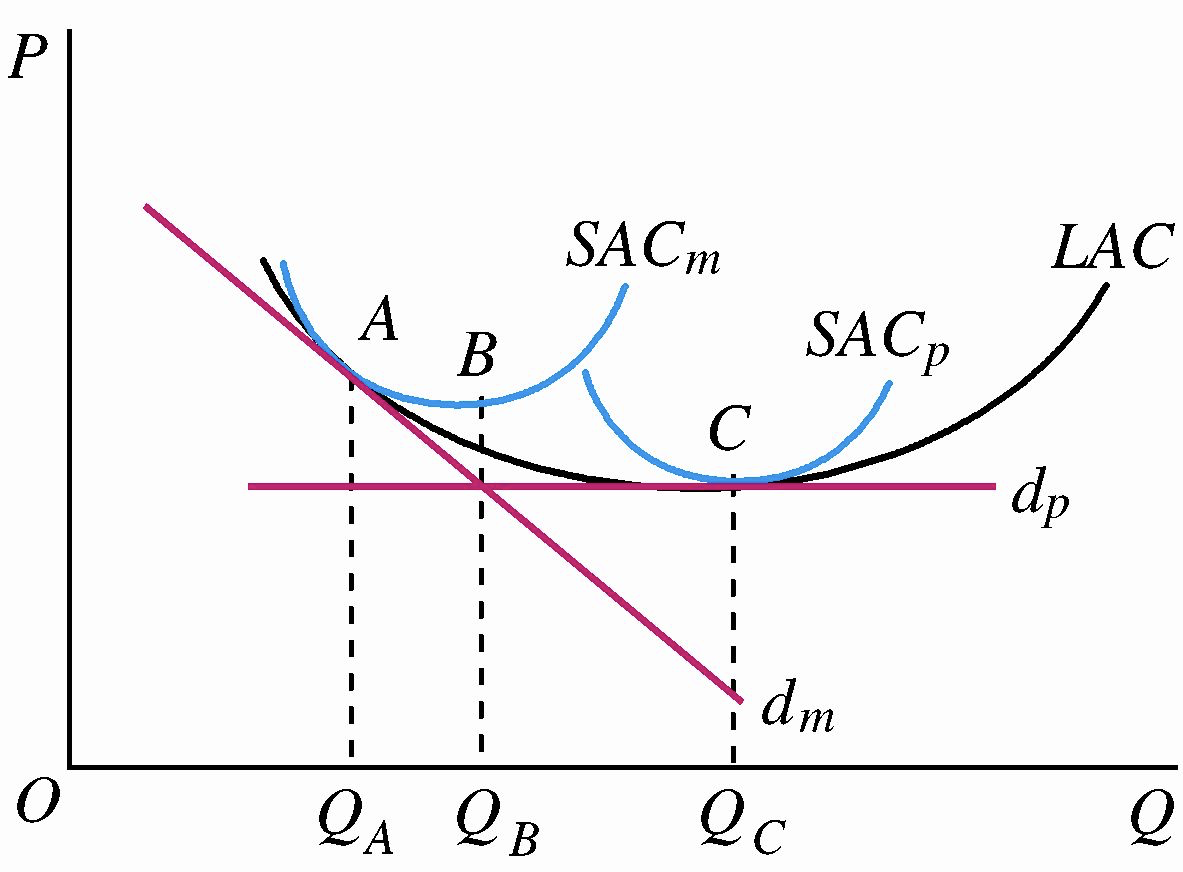
如图所示,垄断竞争厂商的长期均衡产量 \(Q_A\) 小于理想的产量 \(Q_C\),多余的生产能力为 \(Q_C-Q_A\)。
张伯伦(垄断竞争理论创始人之一)认为:多余的生产能力可以代表由于想得到产品的多样化而付出的代价。
也有经济学家认为,多余的生产能力反映在现实经济生活中时生产某些相似产品的小规模企业过于拥挤,垄断竞争生产集团内的商场数量过多。如果减少厂商的数量,单个厂商的生产能力扩大,生产的平均总成本就会下降。
2. 非价格竞争
在完全竞争市场上不存在非价格竞争(因为产品完全同质)。
垄断竞争厂商往往通过改进产品品质、精心设计商标和包装,改善售后服务以及广告宣传等手段来扩大自己产品的市场销售份额,这就是非价格竞争。
非价格竞争的原因:价格竞争虽然能使一部分厂商得到好处,但从长期看,价格竞争会导致产品价格持续下降,最终厂商的超额利润消失。
非价格竞争的基本原则:非价格竞争也需要付出成本,因此需要遵循 \(MC=MR\) 的利润最大化原则。
非价格竞争的作用:
- 强化市场的竞争程度,也满足了消费者的多样化商品与服务的需求。
- 增强了消费者对某些产品的依赖程度,使厂商加强了对自己产品的垄断程度。
对广告的评价:
- 广告分为信息性广告与劝说性广告。
- 信息性广告有利于消费者作出最佳的购买决策,节约消费者的搜寻成本。信息性广告之间的相互竞争,有利于经济资源的合理配置;
- 劝说性广告很少提供对消费者来说真正想获得的信息,虽然可以增加厂商的销售量,但被诱导的消费者往往不能买到自己实际上需要且真正满意的商品。
3. 为何垄断竞争厂商之间倾向于非价格竞争?
- 垄断竞争厂商的产品之间有较大的替代性,因而其需求价格弹性较高,需求曲线接近于水平线。根据斯威齐模型可知,当垄断竞争厂商提高价格时,如其他厂商不跟着提价,他的销售市场会大幅度缩小,使利润反而减少;反之,当垄断竞争厂商降价时,其他厂商也跟着降价,他的销售量只会稍有增加,因此,垄断竞争厂商之间一般不愿意进行价格竞争,而宁可进行非价格竞争。
- 价格竞争虽然能使一部分厂商得到好处,但从长期看,价格竞争会导致产品价格持续下降,最终使厂商的利润消失。另外,政府可能会通过法律或管制的手段来对价格竞争进行干预。
- 非价格竞争指在垄断竞争市场上,由于每一个厂商生产的产品都是有差别的,垄断竞争厂商往往通过改进产品品质、精心设计商标和包装、改善售后服务以及广告宣传等手段,增加消费者对其产品的依赖程度,加强了产品的垄断程度,扩大产品的市场销售份额,获得最大的利润。
非价格竞争的内容要比价格竞争广泛和复杂得多,在采用非价格竞争中,在取得效果与采取行动之间有一个时滞,不会迅速收到效果,作用也不太猛烈,竞争对手对这种竞争方式也不宜觉察到。因此,一个企业一旦通过非价格竞争取得一定效果,其对手就很难再回复到原有的市场份额,要改变这种不利局面,需要花费更多时间和更多资金。
三、寡头垄断市场
(一)概念与分类
1. 概念、特征与原因
1.1 概念
寡头市场/寡头垄断市场:指由少数几家厂商控制整个市场的产品生产和销售的这样一种市场组织。这几家厂商的产量在该行业总产量中各占较大的份额,市场上每个厂商都有举足轻重的作用。
1.2 特征
- 厂商数量极少,新的厂商进入或退出市场比较困难;
- 从事同质产品或差别产品的生产与销售,厂商之间存在激烈竞争;
- 寡头厂商之间的行为相互依存、相互制约;
- 由于寡头厂商之间的相互依存关系,寡头厂商产品的需求曲线就难以确定,厂商行为具有不确定性;
- 除价格竞争外,更经常的是["非价格竞争"]。
1.3 形成原因
- 规模经济
- 对关键生产资源供给的控制
- 专利或专有技术
- 政府特许
2. 分类
根据产品特征:纯粹寡头与差别寡头
根据厂商行动方式:有勾结行为(合作)与无勾结行为(不合作)
根据厂商数量:双头寡头、三头寡头、多头寡头
3. 种类
垄断竞争模型可以分为两类:
- 猜测产量模型:["古诺模型"]、["斯塔克伯格模型"]
- 猜测价格模型:["价格领导模型"]、["斯威齐模型"]
(二)古诺模型(双头模型)
古诺模型(Cournot model)是由法国经济学家奥古斯汀·古诺在 1838 年发表的《对财富理论的数学原理的研究》中提出。
1. 经典的古诺模型
假设条件:
- 市场价格与需求总量之间存在线性关系 \(P=a-bQ\);
- 市场中两个厂商同时决定利润最大化时的产量;
- 单个厂商的产量决策以其他竞争对手产量不变为前提;
- 生产相同的商品,且生产成本为零
具体假设:市场上只有 A、B 两个厂商生产和销售相同的产品,它们的生产成本为零;它们共同面临的市场的需求曲线是线性的, A、B 两个厂商都准确地了解市场的需求曲线;A、B 两个厂商都是在已知对方产量的情况下,各自确定能够给自己带来最大利润的产量,即每一个厂商都是消极地以自己的产量去适应对方已确定的产量。
当生产成本为零,寡头厂商数量为 \(m\),结论为:
每个寡头厂商的均衡产量:\(均衡产量=市场总容量 \times \frac 1 {m+1}\)
行业的均衡总产量:\(总产量=市场总容量 \times \frac m {m+1}\)
2. 求解过程
2.1 市场结构
市场上只有两个厂商生产和销售安全相同的产品,企业决策变量为产量。假定两个企业同时生产,这时市场上的价格 \(P\) 是两个企业产量之和的函数,即需求函数为:\(P=P(q_1 + q_2)\),其中,\(q_1\)、\(q_2\) 分别是企业 1 与企业 2 的产量。
从企业 1 出发进行分析,它估计企业 2 的产量为 \(q_2^e\),若企业 1 决定生产 \(q_1\),则市场上供给的产量为 \(q_1+q_2^e\),相应的市场价格为:\(P(q)=P(q_1 + q_2^e)\),企业 1 的利润最大化问题可以写成:
\[\begin {align} \max _{q_1} \ \{ P(q_1 + q_2^e) \cdot q_1 -C(q_1) \} \end {align} \]2.2 反应函数
结合企业 1 的利润函数可以看出,企业 1 的最佳产出量 \(q_1\) 是其对于企业 2 的产量预期的函数,即:
\[\begin {align} q_1 = f_1(q_2^e) \end {align} \]上式为企业 1 对企业 2 产量的“反应函数”(reaction function),同理,企业 2 也对企业 1 的产量 \(q_1\) 进行估计,在给定企业 1 的产量预期 \(q_1^e\) 的前提下,能得出企业 2 的反应函数为:
\[\begin {align} q_2 = f_2(q_1^e) \end {align} \]2.3 古诺均衡
古诺均衡指产量 \((q_1^*,q_2^*)\) 满足:
\[\begin {align} q_1 ^*= f_1(q_2^*) \\ q_2^* = f_2(q_1^*) \end {align} \]因此,古诺均衡有以下含义:
- 市场供求相等;
- 利润最大化:给定对于另一个企业的产量预期,每一个企业都做出了自己最优的产量选择,使自己利润最大化;
- 理性预期:每一个企业对对方企业的产量预期正确,即 \(q_1^e=q_1^* \),\(q_2^*=q_2^e\),厂商不可能通过改变产量来增加利润;
- 古诺均衡是纳什均衡。
3. 例子
考虑以下古诺竞争模型。市场中有 \(N\) 个企业,生产相同的产品,均没有生产成本。市场需求函数为 \(P=a-bQ\),其中 \(a,b>0\),\(Q\) 为行业总产量。如果企业同时展开产量竞争,那么:
(1)均衡时价格是多少?
(2)此时消费者剩余是多少?
解答:(1)代表性企业 \(i\) 的利润函数为:
\[\begin {align} \pi_i=P q_i =\Bigg [ a-b\sum_{n=1}^N q_n \Bigg] q_i \end {align} \]利润最大化的一阶条件是:
\[\begin {align} \frac {\partial \pi_i} {\partial q_i}= a-b\sum_{n=1}^N q_n - b q_i = 0 \end {align} \]整理可得:
\[\begin {align} b q_i= a-b \sum_{n=1}^N q_n \end {align} \]古诺竞争时生产相同产品的各企业的产量相等,即:\(\sum_{n=1}^N q_n = Nq_i\),联立上式,可以解出各企业的产量为:
\[\begin {align} q_i=\frac a {b(N+1)} \end {align} \]行业总产量为:\(Q=Nq_i=\frac {aN} {b(N+1)}\)
将行业总产量代入需求函数可得:\(P=\frac a {N+1}\)
(2)此时,消费者剩余为:\(CS=\frac 1 2 \times \Big (a-\frac a {N+1} \Big ) \times \frac {aN} {b(N+1)}=\frac {a^2N^2} {2b(N+1)^2}\)
(三)斯塔克伯格模型(产量领导模型)
1. 假设与分析思路
斯塔克伯格(Stackelberg)模型通常用于描述这样一个产业:z 在该产业中存在着一个支配企业,除此之外,该产业中还有若干小企业,那些小企业经常是等待支配企业宣布其产量计划,然后再相应调整自己的产量。因此,斯塔克伯格模型也被称之为“领导者一追随者”模型。
(1)假设条件:
-
产量领袖模型——顺序决策
-
其他假设与["古诺模型"]相同:
- 市场价格与需求总量之间存在线性关系 \(P=a-bQ\);
- 市场中两个厂商同时决定利润最大化时的产量;
- 单个厂商的产量决策以其他竞争对手产量不变为前提;
- 生产相同的商品,且生产成本为零。
(2)分析思路:
- 先分析追随型企业的选择(反应函数);
- 再分析主导企业/领袖企业的选择:将反应函数纳入领导型企业的决策过程,得出领导型企业的最优产量决策。
具体来看:
① 追随者利润最大化:
\[\begin {align} \max _{q_2} P(q_1+q_2) \cdot q_2 - C_2(q_2) \end {align} \]从其中求解追随者的反应函数:\(q_2 = f_2(q_1)\)
② 领导者的利润最大化:
将厂商 2 的反应函数代入领导者利润函数,可得利润函数:
\[\begin {align} \pi_1 = P \big [q_1+f_2(q_2) \big ] \cdot q_1 - C_1(q_1) \end {align} \]得领导者最大化利润的产量选择 \(q_1^* \),再代入追随者的反应函数可得追随者的产量选择 \(q_2^* \),此时市场价格为 \(P^*(q_1^*+q_2^*)\),最后市场均衡为 \(q_1^*+q_2^* \)。
**(3)结论:**先行者得利
2. 例子
若寡头市场的需求曲线为 \(P=30-Q\),两个寡头厂商的边际成本相等,均为 \(MC=3\),无固定成本。
(1)若厂商 1 是产量领导,每个厂商的产量与利润是多少?
(2)若两个厂商串谋,每个厂商的产量与利润是多少?
(3)串谋能否实现?
解答:(1)\(P=30-Q\),\(MC_1=MC_2=3\)
追随者厂商 2 的利润:\(\pi _2 =TR_2-TC_2=[30-(q_1+q_2)]\cdot q_2-3q_2=-q_2^2+(27-q_1)q_2\)
厂商 2 利润最大化决策:\(\frac {d \pi_2} {d q_2} = -2q_2+27-q_1=0\),即反应函数为:\(q_2=13.5-0.5q_1\)
将反应函数代入厂商 1 的利润函数:
\[\begin {align} \pi _1 & = TR_1-TC_1=[30-(q_1+q_2)]\cdot q_1-3q_1 \notag \\ & = [ 30-(q_1+(13.5-0.5q_1) ) ] \cdot q_1-3q_1 \notag \\ & = (13.5-0.5 q_1) q_1 \end {align} \]厂商 1 利润最大化条件:\(\frac {d \pi_2} {d q_2} = -q_1 + 13.5 = 0\),即可解得:\(q_1=13.5\),\(q_2= 6.75\)
厂商 1 的利润:\(\pi_1=91.125\),厂商 2 的利润:\(\pi_2=45.5625\),此时 \(\pi_1>\pi_2\)
(2)若两个厂商串谋,则可以将两个厂商看作一个整体,其利润函数为:
\[\begin {align} \pi=PQ-TC=(30-Q)Q-3Q=-Q^2+27Q \end {align} \]利润最大化时:\(\frac {d\pi} {dQ}=-2Q+27=0\),解得 \(Q=13.5\),此时价格为 \(P=16.5\),\(q_1=q_2=6.75\)
厂商 1 与厂商 2 的利润均为:\(\pi_1=\pi_2=91.125\)
(3)厂商 1 为实现利润最大化,当厂商 2 生产 \(q_2=6.75\) 单位产品时:
如果厂商 1 按照串谋只生产 \(q_1=6.75\),利润为:\(\pi_1=91.125\);
如果厂商 1 破坏协议,此时厂商 1 已知厂商 2 的产量,厂商 1 的反应函数为 \(q_1=13.5-0.5q_2\),即 \(q_1=10.125\),此时总产量 \(Q=16.875\),价格为 \(P=13.125\),此时,厂商 1 利润为 \(\pi_1=102.52\),厂商 2 利润为 \(\pi_2=68.34\)。
也就是说,厂商 1 破坏协议可以获得更高的利润,此时厂商 2 的利润将会降低。
当没有破坏协议的惩罚措施时,厂商 2 不会遵守协议,串谋无法实现。
因此:两个寡头厂商达成卡特尔联盟(松散的价格协议),其结果也是松散的(分分合合)。
卡特尔悖论:
- 有串谋协议时:遵守协议比不遵守协议更好(串谋 > 古诺均衡)
- 无串谋协议时:不遵守协议比遵守协议更好(古诺均衡 > 串谋)
(四)价格领导模型
价格领导模型与古诺模型和斯塔克伯格模型关键不同的是,它选择价格作为决策变量。
**假设:**领导者确定的价格是 \(p\),追随者把 \(p\) 作为既定价格接受,然后选择它的利润最大化产量,领导者根据追随者的选择再做出产量选择。
**结论:**在均衡状态,两家厂商销售同一产品,追随者总是确定与领导者相同的价格。
分析思路:
(1)追随者利润最大化:
\[\begin {align} \max _{q_2} p q_2 - C_2(q_2) \end {align} \]从而得出追随者的供给函数 \(S(p)\)。
(2)领导者利润最大化:
领导者认识到在其定价 \(p\) 时,追随者会供给 \(S(p)\),则它可以出售的产量是 \(R(p)=D(p)-S(p)\),即整个需求在除去追随者供给产量之后的数量。假定领导者有不变的边际生产成本 \(c\),则对于任意价格 \(p\),领导者的利润为:
\[\begin {align} \pi_1 (p)= (p-c)[D(p)-S(p)]= (p-c)R(p) \end {align} \]为使利润最大化,领导者要选择利润最大化 \(MC=MR\) 的价格和产量组合。
(五)斯威齐模型
斯威齐模型 / 弯折的需求曲线模型(Kinked Demand Curve Model),由美国经济学家斯威齐(P.M. Sweezy)于 1939 年提出来,被用来解释一些寡头市场上的价格刚性现象。寡头垄断厂商推测其他厂商对自己价格的态度时“跟跌不跟涨”。该模型的基本假设条件是:如果一个寡头厂商提高价格,行业中的其他寡头厂商都不会跟着改变自己的价格,因而提价的寡头厂商的销售量的减少是很多的;如果一个寡头厂商降低价格,行业中的其他寡头厂商会将价格下降到相同的水平,以避免销售份额的减少,因而该寡头厂商的销售量的增加是很有限的。
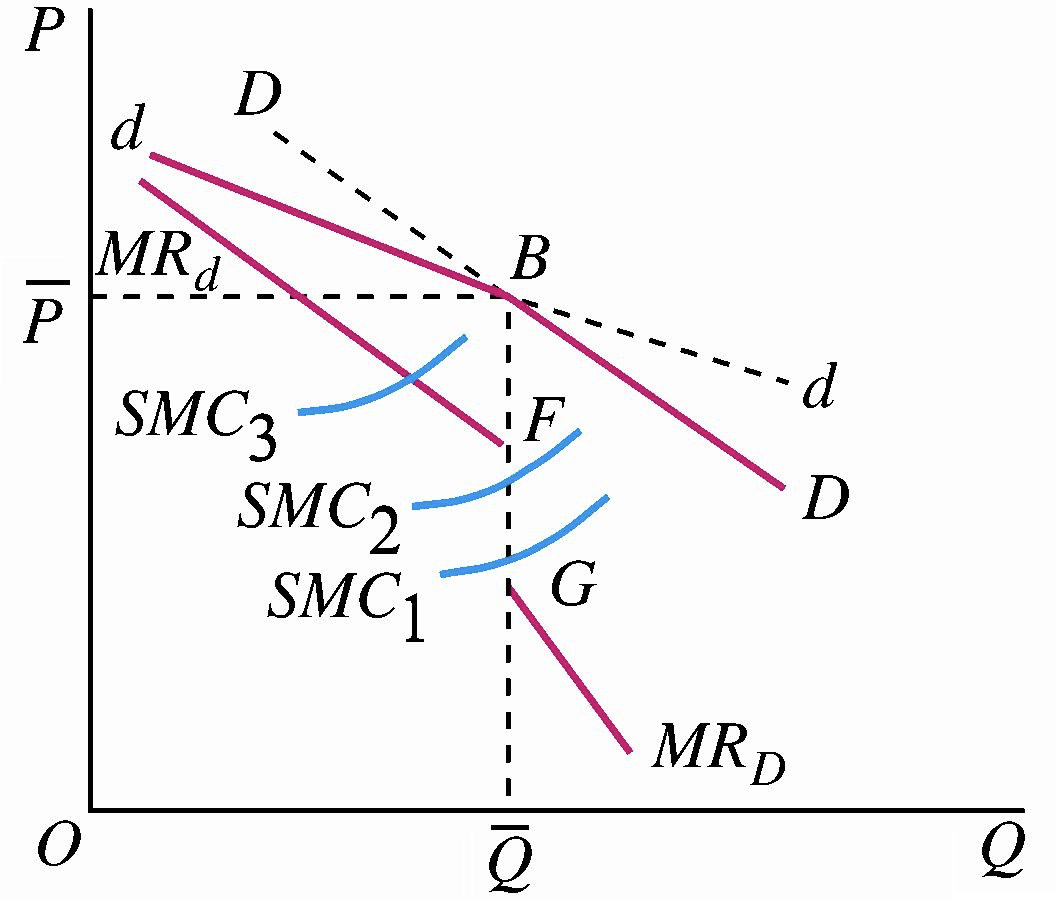
根据这样的假定,寡头厂商的产品需求曲线是弯折的,拐点以上的需求曲线比拐点一下的需求曲线更平坦。弹性不同的拐折需求曲线会形成两条 \(MR\) 曲线,这两条 \(MR\) 曲线在拐折点相关的产量上会出现不连续的空隙。不连续部分的长度取决于拐点上两条需求曲线弹性的差异程度。边际成本在 \(MR\) 的不连续区域变动,不影响均衡价格与均衡产量。只要去喜爱呢与 \(MR\) 曲线相交于 \(MR\) 曲线的不连续区域,寡头厂商都能达到均衡,使产量的变动达到利润极大化。
四、不同市场的比较
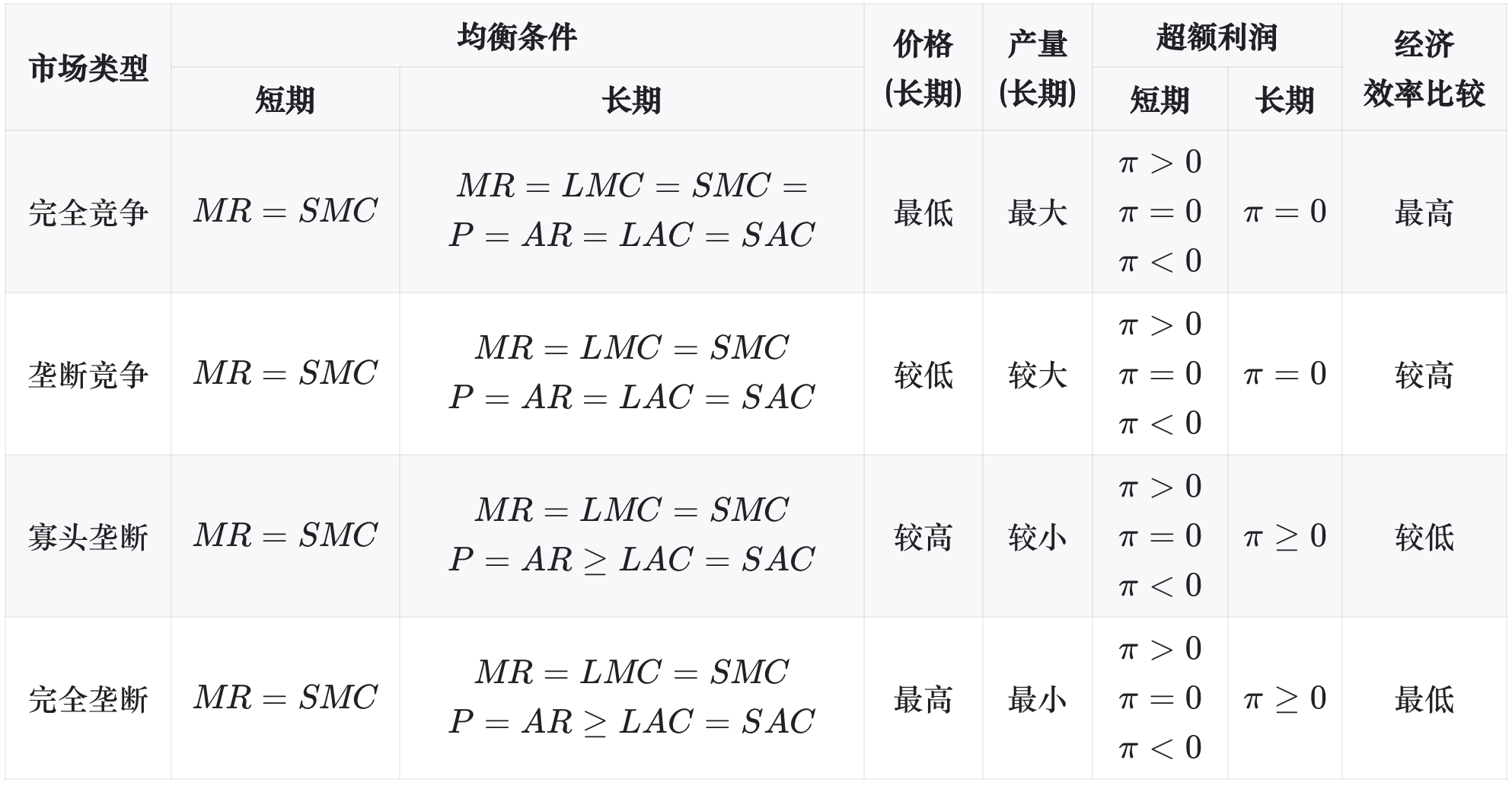
(一)不同市场的长期均衡与条件
1. 经济效率
经济效率指利用经济资源的有效性。
不同市场结构的经济效率是不同的。市场结构直接影响经济效率的高低。完全竞争市场效率最高,垄断竞争市场较高,寡头市场较低,完全垄断市场最低。可见,市场的竞争程度越高,则经济效率越高。
完全竞争市场是经济效率最高的市场。因为当完全竞争场达到长期均衡时该厂商不仅在长期平均成本最低点生产,而且在短期也是平均成本最低点生产。这说明,在完全竞争情况下的生产规模和产量都是适度的,短期平均成本也是最小的。厂商在这种状态下从事生产活动,垄断利润为零。因而社会资源能够得到最佳配置和获得最充分的利用。另外,由于完全竞争的作用,可以使均衡价格降低到最低点,从而消费者也可以从中获得福利,所以完全竞争市场模型被认为是一种理想的经济模型。
完全竞争市场 > 垄断竞争市场 > 寡头市场 > 垄断市场
2. 产量与价格
在不完全竞争市场条件下,厂商的需求曲线是向左下方倾斜的,厂商的垄断程度越高,需求曲线越陡峭。垄断程度越低,需求曲线越平坦。在垄断竞争市场上,厂商长期利润为零,所以在垄断竞争厂商的长期均衡时,厂商需求曲线是向右下方倾斜的,相对比较平坦的需求曲线相切于长期平均成本曲线的最低点左边,产品的均衡价格比较低,但厂商仍存在剩余的生产力。
在垄断市场上,厂商长期内获得利润,所以在垄断厂商的长期均衡时,厂商需求曲线向右下方倾斜的。相对比较陡峭的需求曲线与长期平均成本相交,产品的均衡价格最高,且大于生产的平均成本;产品的均衡数量低,垄断厂商若肯放弃一些利润,价格就可以下降一些,产量就可以增加一些。
在寡头市场上,厂商的需求曲线不太确定,一般认为,寡头市场是与垄断市场是比较相似的市场组织。在长期均衡时,均衡价格比较高,均衡产量比较低。
3. 关于 P=LMC 的条件
\(P=LMC\):资源得到最有效配置(如完全竞争市场)
\(P>LMC\):资源配置不当(如不完全竞争市场)
(传送门:"四种市场的特征比较")

补充:
厂商的经营决策依据:
- 确定产量:\(MR\) 与 \(MC\) 比较
- 是否盈利:\(AR\) 与 \(AC\) 比较
(二)垄断与经济
1. 垄断市场与技术进步(两种观点)
1.1 垄断阻碍技术进步
垄断利润的长期性导致垄断厂商缺乏技术创新的动力。为了防止潜在竞争对手的新技术和新产品对其垄断地位造成威胁,垄断厂商有可能通过各种方式去阻碍技术进步。
1.2 垄断有利于技术进步
垄断厂商利用高额利润所形成的雄厚经济实力,有条件进行各种科学研究和重大的技术创新。垄断厂商可以利用垄断地位,在长期内保持由于技术进步而带来的更高利润。
2. 规模经济
对不少行业而言,只有大规模的生产,才能获得规模经济的好处,而这往往只有在寡头市场与垄断市场条件下才能做到(如:钢铁与铁路运输)。
3. 产品差别
在完全竞争市场条件下,所有厂商的产品都是完全相同的,无法满足消费者的各种偏好。
在垄断竞争的市场条件下,众多厂商之间的产品有差别,多样化的产品使消费者有更多的选择自由,可满足不同的需要。但是,产品的一些虚假的非真实性的差别,也会给消费者带来损失。
4. 广告支出
一方面,垄断竞争市场与产品差别寡头市场的大量广告位消费者提供了信息。
另一方面,过于庞大的广告支出会造成资源浪费与销售价格的抬高,再加上某些广告内容的夸张和诱导,对消费者是不利的。